Tam giác ABC có ˆA=105∘A^=105∘, ˆB=45∘B^=45∘, BC = 4cm. Tính độ dài các cạnh AB, AC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DT
1
Những câu hỏi liên quan
PT
1
CM
15 tháng 4 2017
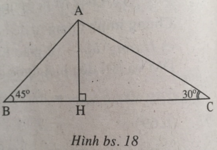
Vẽ đường cao AH. Đặt BH = x, CH = y thì do H nằm giữa B và C (hai góc ∠ B, ∠ C là góc nhọn) suy ra x + y = 4 (xem h.bs.18).
Ta có BH = AH = HC.tg 30 ° nên x – y.tg 30 ° = y/ 3
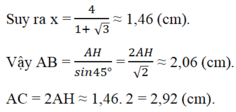
AC = 2AH ≈ 1,46. 2 = 2,92 (cm).
NB
1
S
2 tháng 7 2017
ABH^ = 45* và AHB^ = 90* => AHB là tam giác vuông cân
=> AH = BH (1)
ACH^ = 180* - A^ - B^ = 180* - 105* - 45* = 30*
=> AH = AC/2 => AC = 2AH
BC = CH + BH = 4 => CH = 4 - BH (2)
(1) và (2) => CH = 4 - AH
AC^2 = CH^2 + AH^2
4AH^2 = (4 - AH)^2 + AH^2
4AH^2 = 16 - 8AH^2 + AH^2 + AH^2
<=> 2AH^2 + 8AH - 16 = 0
<=> AH^2 + 4AH - 8 = 0
=> AH = 2(√3 -1)
=> AB^2 = 2AH^2 = 2.4(3 - 2√3 + 1) = 8(4 - 2√3) = 16(2 - √3)
=> AB = 4√(2 - √3)
AC = 2AH = 4(√3 -1)
S
2 tháng 7 2017
bạn nên nhớ 2 công thức sau:
+ trong tam giác có góc A = 60độ thì ta có: BC² = AB² + AC² - AC.AB.
+ trong tam giác có góc A = 120độ thì ta có: BC² = AB² + AC² + AC.AB.
Giải: Kẻ đường cao BH của ∆ABC. xét tam giác ABH vuông tại H, có góc BAH = 60độ => góc ABH = 30độ => AB = 2.AH (bổ đề: trong tam giác vuông có góc = 30độ, thì cạnh đối diện với góc 30độ = nửa cạnh huyền - c/m không khó)..
Xét ∆BHC vuông tại H => BC² = BH² + HC² = BH² + (AC - AH)²
= BH² + AH² + AC² - 2.AH.AC
= (BH² + AH²) + AC² - AB.AC (vì AB = 2AH)
= AB² + AC² - AB.AC => ta đã c/m đc. công thức 1. Thay AB = 28cm và AC = 35cm vào ta tính được BC = √1029 (cm) ≈ 32,08 (cm)
Công thức 2 thì cách chứng minh cũng khá giống, cũng kẻ đường cao từ B. Tự chứng minh nha bạn ^^
Vẽ đường cao AH . Đặt BH = x, CH = y thì do H nằm giữa B và C ( hai góc \(\widehat{B } ; \widehat{C}\) là góc nhọn) suy ra x + y = 4
Ta có \(BH=AH=HC.tg30^o\)nên \(x-y.tg30^o=y\sqrt{3}\)
\(\Rightarrow x=\frac{4}{1+\sqrt{3}}\approx1,46\left(cm\right)\)
Vậy \(AB=\frac{AH}{\sin45^o}=\frac{2AH}{\sqrt{2}}\approx2,06\left(cm\right)\)
\(AC=2AH\approx1,46.2=2,92\left(cm\right)\)
AC = 2AH ≈ 1,46. 2 = 2,92 ( cm )