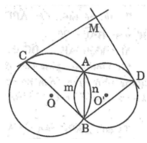
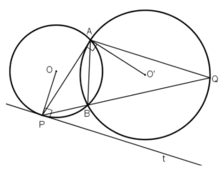
*Bài 1: Hai đường tròn (O) và (O') cắt nhau tại A và B. Đường thẳng qua A cắt đường tròn (O) tại điểm C và cắt đường tròn (O') tại điểm D
a) Chứng minh khi đường thẳng quay quanh A thì \(\widehat{CBD}\)có sđ không đổi
b) Từ C và D vẽ 2 tiếp tuyến với đường tròn. CMR góc tạo bởi 2 tiếp tuyến này có số đo không đổi khi cát tuyến CAD quay quanh A
*Bài 2: Từ điểm M ở ngoài đường tròn (O), kẻ tiếp tuyến MT (T là tiếp điểm) và cát tuyến MAB qua O ( A,B\(\in\)đường tròn, A ở giữa M và D). CM: \(\widehat{AMT}+\widehat{MTA}=90^o\)