Giúp mình ba bài này nhanh với...
Đọc tiếp
Giúp mình ba bài này nhanh với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 6 2023
Đặt A=1/3+2/3^2+...+100/3^100
=>3A=1+2/3+...+100/2^99
=>3A-A=1+(2/3-1/3)+(3/32-2/32)+...(100/299-99/2^99)-100/3100
=>2A=1+1/3+1/3+1/32+...+1/399-100/3100
Ta lại đặt tiếp B=1/3+...+1/399
tiếp tục làm 3B=1+...+1/398
=>3B-B=1+...+1/398-1/3+...+1/399=1-1/3^99
=>B=(1-1/3^99)/2 (đến đây viết mũ là ^ vì lười)
đến đây ta có 2A=1+(1-1/3^99)/2 -100/3^100
=(3^100-100)/3^100 +(1-1/3^99)/2
quy đồng lên nó thành
2A=2x3^100-200/3^100x2 +(3^99-1)/3^99x2
2A=(2x3^100-200+3^100-3)/3^100x2
=(3^101-203)/3^100x2
ta c/m 2a<3/2 là ok
*nhân chéo lên =>2(3^101-203)<3^101x2
đồng nghĩa với 2x3^101 -406<3^101x2 (điều này luôn đúng)
=>bài toán đc chứng minh
TT
15 tháng 10 2017
\(\left(x-1\right)^5=-32\)
\(\Leftrightarrow\left(x-1\right)^5=\left(-2\right)^5\)
\(\Rightarrow x-1=-2\)
\(\Rightarrow x=-2+1\)
\(\Rightarrow x=-1\)
15 tháng 10 2017
(x-1)5= -32
=>(x-1)5=(-2)5
=> x-1 = -2
=> x = -2 +1
=> x = -1.
VH
1
LM
Lê Minh Vũ
CTVHS
14 tháng 6 2023
\(2.16\ge2^n>4\)
\(2.2^4\ge2^n>2^2\)
\(2^5\ge2^n>2^2\)
=> \(n\in\left\{3,4,5\right\}\)
Vậy: \(n\in\left\{3,4,5\right\}\)
1 tháng 9 2021
a: Ta có: \(2\sqrt{28}+3\sqrt{63}-3\sqrt{\dfrac{112}{9}}-\sqrt{\dfrac{196}{7}}\)
\(=4\sqrt{7}+9\sqrt{7}-4\sqrt{7}-2\sqrt{7}\)
\(=7\sqrt{7}\)
b: Ta có: \(\sqrt{8+2\sqrt{7}}-\sqrt{12-\sqrt{140}}-\sqrt{5}\)
\(=\sqrt{7}+1-\sqrt{7}+\sqrt{5}-\sqrt{5}\)
=1
25 tháng 2 2022
Dạng 4: Toán lượng dư:
Bài 1:nBr2=0,05x0,5=0,025 (mol)
PTHH: 2NaI+Br2→2NaBr+I2
0,025 0,05 (mol)
→ mNaBr=0,05.103= 5,15 (g)
Chúc em học giỏi
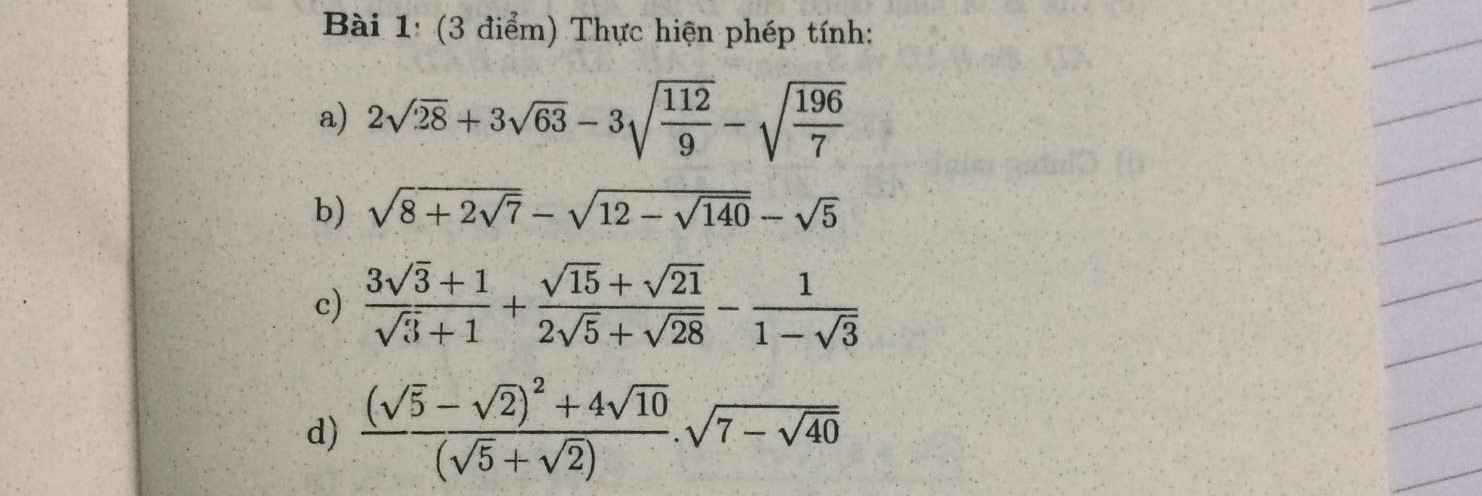
Bài 1:
Ta có: \(A=\dfrac{x}{yz}:\dfrac{y}{zx}=\dfrac{x}{yz}.\dfrac{zx}{y}=\dfrac{x^2}{y^2}=\left(\dfrac{x}{y}\right)^2\)
Mà \(3x=2y\Leftrightarrow\dfrac{x}{y}=\dfrac{2}{3}\Leftrightarrow\left(\dfrac{x}{y}\right)^2=\dfrac{4}{9}\)
\(\Rightarrow A=\dfrac{4}{9}\)
\(1,\\ 3x=2y\Rightarrow\dfrac{x}{y}=\dfrac{2}{3}\Rightarrow\dfrac{x}{yz}=\dfrac{2}{3z}\\ 3x=2y\Rightarrow\dfrac{y}{x}=\dfrac{3}{2}\Rightarrow\dfrac{y}{zx}=\dfrac{3}{2z}\)
\(2,\\ \dfrac{x}{y^2}=2\Rightarrow x=2y^2\\ \dfrac{x}{y}=16\Rightarrow x=16y\\ \Rightarrow2y^2=16y\Rightarrow2y\left(y-8\right)=0\\ \Rightarrow\left[{}\begin{matrix}y=0\left(ktm.vì.y\ne0\right)\\y=8\end{matrix}\right.\Rightarrow y=8\Rightarrow x=128\)
\(3,\\ \dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a-b}{c-d}\Rightarrow\dfrac{a-b}{b}=\dfrac{c-d}{d}\)