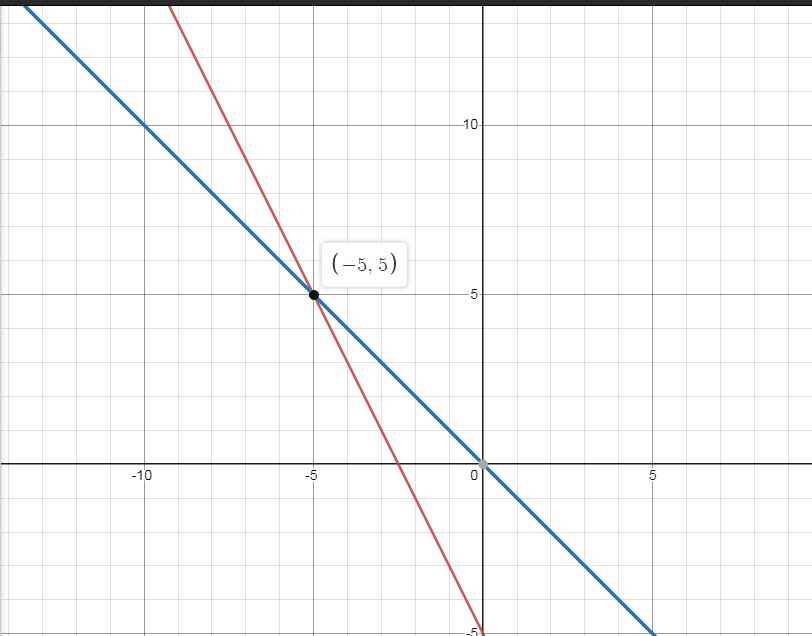
cho hai hàm số bậc nhất y=-2x+5 (d) và y=0,5x (d')
a) vẽ đồ thị (d) và (d') của 2 hàm số đã cho trên cùng 1 hệ tọa độ Oxy
b) tìm tọa độ điểm M là giao điểm của 2 đồ thị vừa vẽ ( bằng phép tính )
c) Tính góc α tạo bởi đường thẳng d với trục hoành Ox ( làm tròn kết quả đến độ)
d) Gọi giao điểm của d với trục Oy là A, tính chu vi và diện tích tam giác MOA