cho\(\Delta ABC\) cân tại A. Gọi D, E, F lần lượt là trung điểm của AB, AC, BC
1) Lấy O đối xứng với F qua E. Chứng minh AFCO là hình chữ nhật
2)Gọi P là giao điểm của DO và AE,Gọi Q là giao điểm của DC và FE. Chứng minh
a) Tứ giác ADEO là hình bình hành
b)PQ \(\perp\)DE

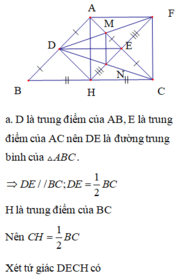


1) ΔABC cân tại A ; AF là trung tuyến ( F là trung điểm BC )
\(\Rightarrow\) AF đồng thời là đường cao \(\Rightarrow\) \(\widehat{AFC}\) = 90\(^O\)
Xét tứ giác AFCO có :
AE = EC ( E là trung điểm AC )
EF = OE ( O đối xứng với F qua E )
AC \(\cap\) OF = \(\left\{E\right\}\)
\(\Rightarrow\) AFCO là hình bình hành
mà \(\widehat{AFC}\) = 90O (cmt) \(\Rightarrow\) AFCO là hình chữ nhật
2) a) Xét ΔABC có :
BF = CF ( F là trung điểm BC )
AE = CE ( E là trung điểm AC )
\(\Rightarrow\) EF là đường trung bình ΔABC
\(\Rightarrow\) EF // AB ; EF = \(\dfrac{1}{2}\) AB ( Tính chất đường trung bình trong tam giác )
CMTT : DE là đường trung binh ΔABC
\(\Rightarrow\) DE // BC ( Tính chất đường trung bình tỏng tam giác )
EF = EO = \(\dfrac{1}{2}\) AB ( cmt ) ; AD = \(\dfrac{1}{2}\) AB ( D là trung điểm AB )
\(\Rightarrow\) EO = AD
Xét tứ giác ADEO có :
EO = AD ( cmt )
EO // AD ( EF // AD )
\(\Rightarrow\) ADEO là hình bình hành \(\Rightarrow\) AP = EP
CMTT : DECF là hình bình hành \(\Rightarrow\) EQ = FQ
b) DE // BC (cmt) ; AF\(\perp\)BC ( \(\widehat{AFC}\) = 90O )
\(\Rightarrow\) DE \(\perp\) AF
Xét ΔAEF có :
AP = EP (cmt)
EQ = FQ (cmt)
\(\Rightarrow\) PQ là đường trung bình ΔAEF
\(\Rightarrow\) PQ // AF (Tính chất đường trung bình trong tam giác)
mà DE \(\perp\) AF (cmt) \(\Rightarrow\) PQ \(\perp\) DE