Cho tam giác ABC cân tại A( AB=AC), AB=8cm,BC=4cm, hai đường cao BD,CE. Tính DE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân

Làm theo cách lớp 8:
Từ A kẻ AH _|_ BC (H nằm trên BC)
Mà tam giác ABC cân tại A => AH đồng thời là trung tuyến => BH = HC = 1cm
Xét tam giác AHB vuông tại H
=> AH2 = AB2 - BH2 = 42 - 12 = 15cm
=> \(AH=\sqrt{15}cm\)
ΔAHC ~ ΔBDC (g.g) vì:
+ Góc C chung
+ \(\widehat{AHC}=\widehat{BDC}=90^0\)
=> \(\frac{AH}{AC}=\frac{BD}{BC}\Rightarrow BD=\frac{AH.BC}{AC}=\frac{2\sqrt{15}}{4}=\frac{\sqrt{15}}{2}cm\)
Vậy \(BD=\frac{\sqrt{15}}{2}cm\)
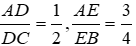

Kẻ đường cao AD.
Có: DB=DC=\(\dfrac{4}{2}=2\left(cm\right)\)
Xét \(\Delta_vABD\), có: \(\cos ABC=\dfrac{BD}{AB}=\dfrac{2}{8}=\dfrac{1}{4}\)\(\Rightarrow\)\(\widehat{ABC}\approx76^o\)
Có: \(\Delta_vDBC=\Delta_vECB\left(ch-gn\right)\)(\(\widehat{ABC}=\widehat{ACB}\left(gt\right);BC\): chung)
\(\Rightarrow BD=CE=BC.\cos ABC=4.\cos76^o\)\(\approx0,97\left(cm\right)\)\(\Rightarrow AD=AE=8-0,97=7,03\left(cm\right)\)\(\Rightarrow\Delta ADE\) cân tại A.
Xét \(\Delta ADE\) và \(\Delta ABC\)\(\widehat{A}\)có: \(\widehat{A}\):chung.
\(\Rightarrow\Delta ADE\sim\Delta ABC\left(gn\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{DE}{BC}\)
hay: \(\dfrac{7,03}{8}=\dfrac{DE}{4}\Rightarrow DE=\dfrac{7,03.4}{8}=3,515\left(cm\right)\)
Bạn ơi , lp 8 đã học cos đâu ...