9991/9992+1/9-2/19984-5/495
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(-\frac{9991}{9992}+\frac{1}{99}-\frac{2}{19984}-\frac{5}{495}\)
\(=-\frac{9991}{9992}+\frac{1}{99}-\frac{1}{9992}-\frac{1}{99}\)
\(=\left(-\frac{9991}{9992}-\frac{1}{9992}\right)+\left(\frac{1}{99}-\frac{1}{99}\right)\)
\(=-1+0\)
\(=-1\)

Thêm bớt 8 để lên thành 100, 1000, ..., 1000...000
Sau khi làm,
A = 100 + .... + 1000...000
=> 10A = ...
=> Trừ ngược còn 9A
=> A
Sau đó trừ đi đống số 8 đã thêm ở đầu nhé

2 < 3
4 < 8
9 < 34
56 < 78
91 < 9999
9991 < 999999999

\(101^2=\left(100+1\right)^2=10000+200+1=10201\)
\(1001^2=\left(1000+1\right)^2=1000000+2000+1=1002001\)
\(102^2=\left(100+2\right)^2=10000+400+4=10404\)
\(99^2=\left(100-1\right)^2=10000-200+1=9801\)
\(19^2=\left(10+9\right)^2=100+180+81=361\)
\(999^2=\left(1000-1\right)^2=1000000-2000+1=998001\)


Số các số hạng của dãy S là:
(497-1):2+1= 249 (số hạng)
Ta cứ nhóm 4 số vào một nhóm thì sẽ được (249:4=62 nhóm) và dư ra số 497. Ta sẽ được:
S= (1+3-5-7)+(9+11-13-15)+........+(489+491-493-495)+497
=(-8)+(-8)+...........+(-8)+497 (62 số -8)
= (-8).62+497
=-496+497
=1


a) Ta có :
\(889=900-1\)
\(=30^2-1\)
\(=\left(30+1\right)\left(30-1\right)\)
\(=31.29\)
b) \(9991=10000-9\)
\(=100^2-3^2\)
\(=\left(100+3\right)\left(100-3\right)\)
\(=103.97\)
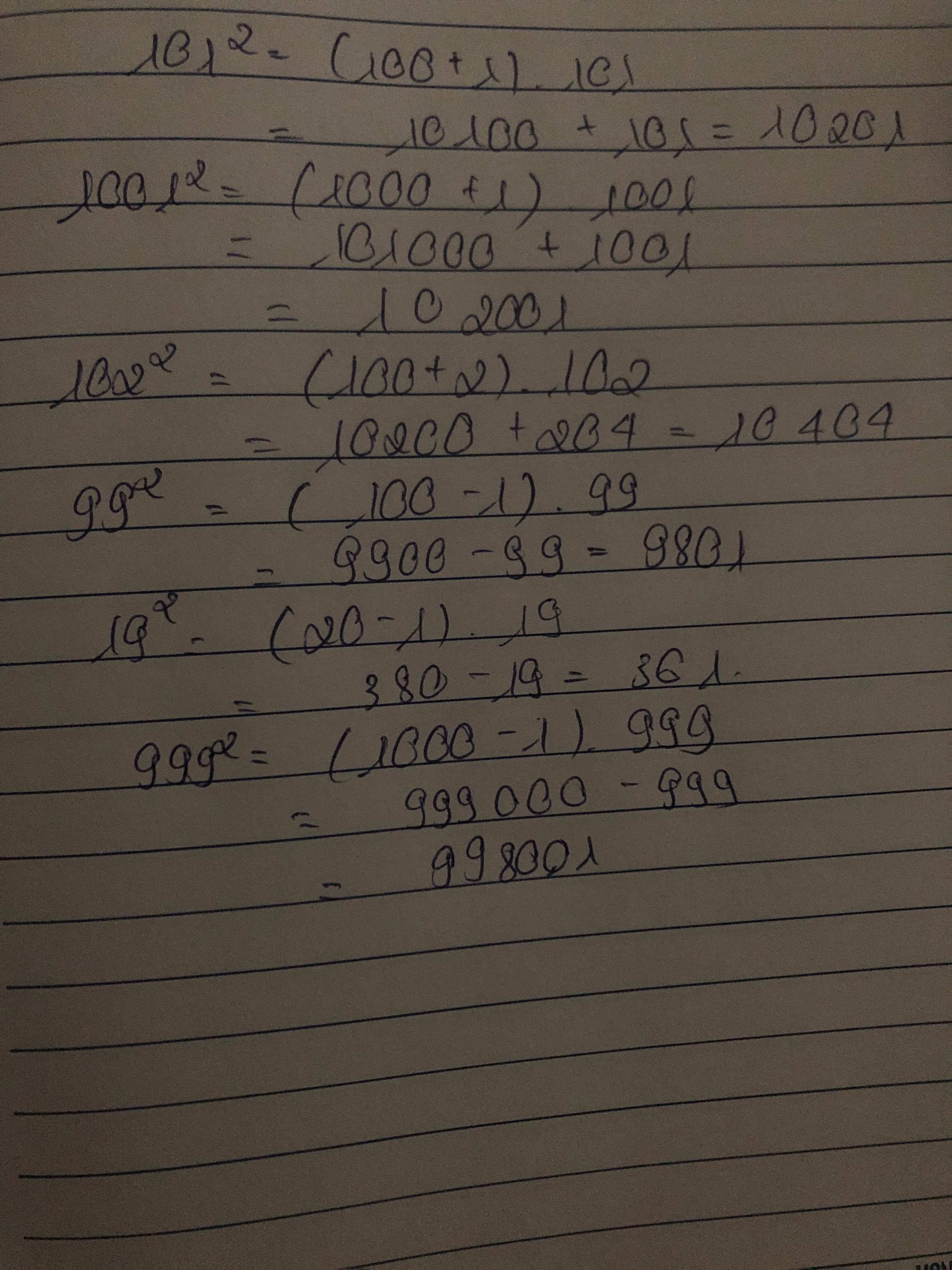
1.100809941\(:>\)
\(\frac{9991}{9992}+\frac{1}{9}-\frac{2}{19984}-\frac{5}{495}\)
\(=0,99989991993+0,11111111111-0,00010008006-0,0101010101\)
\(=1,10080994088\)