Xét △ ADC và  △ BEC, ta có:

∠ (ADC) = ∠ (BEC) = 90 0

∠ C chung

Suy ra:  △ ADC đồng dạng  △ BEC (g.g)

Suy ra: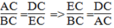 ⇒ ECBC = DCAC

Xét  △ DEC và  △ ABC ta có:

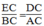
∠ C chung

Vậy  △ DEC đồng dạng  △ ABC (c.g.c)

câu 1 : vì MN là đường TB của tam giác ABC => MN // BC nên theo hệ quả định lí ta-lét , ta có :

\(\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\)
=> tam giác ABC đồng dạng với tam giác AMN theo trường hợp cạnh cạnh cạnh

Xét ΔABD vuông tại D và ΔCHD vuông tại D có

góc BAD=góc HCD

=>ΔABD đồng dạng vớiΔCHD

a) Xét t/giác HBA và t/giác ABC

có: \(\widehat{B}\):chung

 \(\widehat{BHA}=\widehat{A}=90^0\)(gt)

=> t/giác HBA đồng dạng t/giác ABC (g.g)

b) Xét t/giác ABC vuông tại A, ta có:

BC² = AB² + AC² (định lí Pi - ta - go)

=> AC² = BC² - AB² = 10² - 6² = 64

=> AC = 8 (cm)

Ta có: t/giác HBA đồng dạng t/giác ABC

=> HB/AB = AH/AC = AB/BC

hay HB/6 = AH/8 = 6/10 = 3/5

=> \(\hept{\begin{cases}HB=\frac{3}{5}.6=3,6\left(cm\right)\\AH=\frac{3}{5}.8=4,8\left(cm\right)\end{cases}}\)

c) Xét tứ giác AIHK có \(\widehat{A}=\widehat{AKH}=\widehat{AIH}=90^0\)

=> AIHK là HCN => \(\widehat{AIK}=\widehat{AHK}\)(cùng = \(\widehat{IKH}\)) (1)

Ta có: \(\widehat{AHK}+\widehat{KHC}=90^0\)(phụ nhau)

 \(\widehat{KHC}+\widehat{C}=90^0\)(phụ nhau)

=> \(\widehat{AHK}=\widehat{C}\) (2)

Từ (1) và )2) => \(\widehat{AIK}=\widehat{C}\)

Xét t/giác AKI và t/giác ABC

có: \(\widehat{A}=90^0\): chung

 \(\widehat{AIK}=\widehat{C}\)(cmt)

=> t/giác AKI đồng dạng t/giác ABC
=> AI/AC = AK/AB => AI.AB = AK.AC 

d) Do AD là đường p/giác của t/giác ABC =>  \(\frac{AB}{AC}=\frac{BD}{DC}=\frac{BC-DC}{DC}=\frac{BC}{DC}-1\)

<=> \(\frac{10}{DC}-1=\frac{6}{8}\) <=> \(\frac{10}{DC}=\frac{7}{4}\) <=> \(DC=\frac{40}{7}\)(cm)

=> BD = 10 - 40/7 = 30/7 (cm)

DE là đường p/giác của t/giác ABD => \(\frac{AD}{BD}=\frac{AE}{EB}\)(t/c đg p/giác)

DF là đường p/giác của t/giác ADC => \(\frac{DC}{AD}=\frac{FC}{AF}\)

Khi đó: \(\frac{EA}{EB}\cdot\frac{DB}{DC}\cdot\frac{FC}{FA}=\frac{AD}{DB}\cdot\frac{AB}{AC}\cdot\frac{DC}{AD}=\frac{AB\cdot DC}{BD.AC}=\frac{6\cdot\frac{40}{7}}{8\cdot\frac{30}{7}}=1\) (ĐPCM)