Cho đoạn thẳng AB . Vẽ 2 đường tròn có bán kính bằng nhau tâm tại A và B sao cho chúng cắt nhau tại M và N .
a) Chứng minh rằng tam giác AMN = tam giác BMN
b) Chứng minh rằng MN là đường trung trực của đoạn thẳng AB
Mình đang cần gấp . Mọi người trả lời giúp mình với nha !!!
Thanks <3333


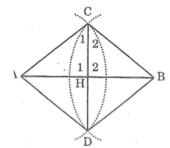
a) Vì hai đường tròn tâm A và B có bán kính bằng nhau nên AM = AN = BM = BN
Xét \(\Delta AMN\)và \(\Delta BMN\)
AM = BM (cmt)
AN = BN (cmt)
MN: cạnh chung
Suy ra \(\Delta AMN\)\(=\Delta BMN\left(c-c-c\right)\)
b) Gọi O là giao điểm của AB và MN
Dễ chứng minh được: \(\widehat{NAB}=\widehat{MBA}\)
Mà 2 góc này ở vị trí so le trong nên \(AN//BM\)
C/m: \(\Delta AON=\Delta BOM\left(g-c-g\right)\)
\(\Rightarrow OA=OB\)(hai cạnh tương ứng)
Sau đó c/m \(AB\perp MN\)suy ra MN là đường trung trực của AB