Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
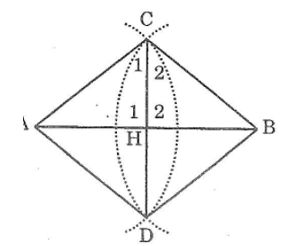
Bài 1:
Gọi H là giao điểm của AB và CD
Nối AC, AD,BC,BD
Xét ΔACD và ΔBCD, ta có:
AC = BC
(bán kính hai cung tròn bằng nhau)
AD = BD
CD cạnh chung
Suy ra: ΔACD= ΔBCD(c.c.c)
Suy ra: ∠C2 =∠C2 (hai góc tương ứng)
Xét hai tam giác AHC và BHC. Ta có:
AC = BC (bán kính hai cung tròn bằng nhau)
∠C2 =∠C2 (chứng minh trên)
CH cạnh chung
Suy ra: ΔAHC= ΔBHC(c.g.c)
Suy ra: AH = BH (hai cạnh tương ứng) (1)
Ta có : ∠H1 =∠H2 (hai góc tương ứng)
∠H1 + ∠H2 =180° (hai góc kề bù)
Suy ra: ∠H1 =∠H2 =90° => CD ⊥ AB (2)
Từ (1) và (2) suy ra CD là đường trung trực của AB
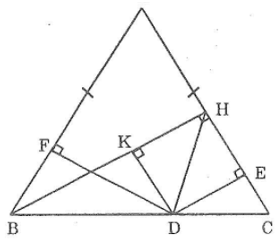
bài 2
Kẻ DK ⊥ BH
Ta có: BH ⊥AC(gt)
Suy ra: DK // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song)
=> ∠KDB =C (hai góc đồng vị)
VìΔABC cân tại A nên ∠B =∠C (tính chất tam giác cân)
Suy ra: ∠KDB =B
Xét hai tam giác vuông BFD và DKB, ta có:
∠BFD =∠DKB
BD cạnh huyền chung
∠FBD =∠KDB (chứng minh trên)
Suy ra:ΔBFD=ΔDKB(cạnh huyền góc nhọn)
=> DF = BK (hai cạnh tương ứng)(1)
Nối DH. XétΔDEHvàΔDKH, ta có:
∠DEH =∠DKH =90°
DH cạnh huyền chung
∠EHD =∠KDH (hai góc so le trong)
Suy ra:ΔDEH=ΔDKH( cạnh huyền , góc nhọn)
Suy ra: DE = HK ( hai cạnh tương ứng) (2)
Mặt khác : BH = BK + KH (3)
Từ (1), (2) và (3) suy ra: DF = DE = BH

Bài 1 :
Xét tam giác ABC và ADE có :
góc EAD = góc CAB (đối đỉnh)
CA=EA (gt)
BA=DA (gt)
suy ra tam giác ABC=ADE (c.g.c)
suy ra :DE =BC ( 2 cạnh tương ứng ) ; góc E= góc C ; góc D = góc B (các góc tương ứng )
Mà M; N lần lượt là trung điểm của DE và BC suy ra EN=DN=BM=CM
Xét tam giác ENA và CMA có:
EN = CM ( cmt)
góc E = góc C (cmt)
AE = AC (gt)
suy ra tam giác EAN = CMA (c.g.c) suy ra AM =AN ( 2 cạnh tương ứng )
Xét tam giác NDA và MBA có:
góc D= góc B (cmt)
ND = MB (cmt )
DA = BA (cmt )
suy ra tam giác NDA = MBA (c.g.c)suy ra góc NAD = góc MAB
Ta có góc DAC +MAC+MAB = 180 độ ( vì D nằm trên tia đối của tia AB )
Mà góc NAD = góc MAB suy ra góc DAC+MAC+NAD =180 độ
suy ra 3 điểm M,A,N thẳng hàng (2)
Từ (1) và (2 ) suy ra A là trung điểm của MN
( mình vẽ hình hơi xấu , mong bạn thông cảm . Nếu đúng nhớ kết bạn với mình nhé , mong tin bạn ^-^)

Bài 3:
Xét ΔHMB vuông tại H và ΔKMC vuông tại K có
MB=MC
\(\widehat{HMB}=\widehat{KMC}\)
Do đo: ΔHMB=ΔKMC
Suy ra: BH=CK

ta có B,C đối xứng nhau qua EM nên
BE=CE
mà rõ ràng CE< CD
Nên BE<CD


a) Vì hai đường tròn tâm A và B có bán kính bằng nhau nên AM = AN = BM = BN
Xét \(\Delta AMN\)và \(\Delta BMN\)
AM = BM (cmt)
AN = BN (cmt)
MN: cạnh chung
Suy ra \(\Delta AMN\)\(=\Delta BMN\left(c-c-c\right)\)
b) Gọi O là giao điểm của AB và MN
Dễ chứng minh được: \(\widehat{NAB}=\widehat{MBA}\)
Mà 2 góc này ở vị trí so le trong nên \(AN//BM\)
C/m: \(\Delta AON=\Delta BOM\left(g-c-g\right)\)
\(\Rightarrow OA=OB\)(hai cạnh tương ứng)
Sau đó c/m \(AB\perp MN\)suy ra MN là đường trung trực của AB