Bạn tự vẽ hình.

a) CD vuông góc AB => CH = DH = 6.   Ta có: HA.HB = CH² \(\Rightarrow HA\left(13-HA\right)=36\Leftrightarrow HA^2-13HA+36=0\)

\(\Leftrightarrow\left(HA-9\right)\left(HA-4\right)=0\Leftrightarrow\)HA = 9 hoặc HA = 4 => HB = 4 hoặc HB = 9

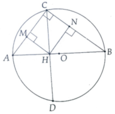
a, Tính được HA=4cm; HB=9cm

b, Tính được HA=4cm; HB=9cm

c, Tính được HM =  12 13 13 cm, HN = 18 13 13 cm

Từ đó tính được S C M H N = 216 13 c m 2

a) Xét ΔANH và ΔAHC có:

∠(NAH) chung

∠(ANH) = ∠(AHN) = 90o

⇒ ΔANH ∼ ΔAHC (g.g)

b) Ta có :

Tương tự : CH = 5 (cm)

⇒ BC = BH + CH = 9 + 5 = 14 (cm)

c) Theo chứng minh trên ta có:

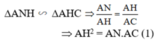
Chứng minh tương tự ta có :

ΔAMH ∼ ΔAHB ⇒ AH2 = AM.AB (2)

Từ (1) và (2) ⇒ AN.AC = AM.AB (3)

Xét ΔAMN và ΔACB có :

∠A chung

AN.AC = AM.AB

⇒ ΔAMN ∼ ΔACB (c.g.c)

d) Ta có : ΔAMH ∼ ΔAHB

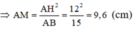
Lại có ΔAMN ∼ ΔACB (cmt)

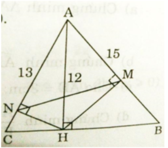
a) Ta có : 

\(BC^2=AB^2+AC^2\left(Pitago\right)\)

\(\Leftrightarrow AC^2=BC^2-AB^2=169-25=144\)

\(\Leftrightarrow AC=12\left(cm\right)\)

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)

\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{AB^2.+AC^2}{AB^2.AC^2}\)

\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{BC^2}{\left(AB.AC\right)^2}\)

\(\Leftrightarrow AH^2=\dfrac{\left(AB.AC\right)^2}{BC^2}=\dfrac{\left(5.12\right)^2}{13^2}\)

\(\Leftrightarrow AH=\dfrac{5.12}{13}=\dfrac{60}{13}\sim4,85\left(cm\right)\)

\(sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{13}\Rightarrow\widehat{B}\sim67^o\)

 a) ∆ABC vuông tại A (gt)

BC² = AB² + AC² (Pytago)A

⇒ AC² = BC² - AB²

= 13² - 5²

= 144

⇒ AC = 12 (cm)

Ta có:

AH.BC = AB.AC

⇒ AH = AB.AC : BC

= 5.12 : 13

= 60/13 (cm) ≈ 4,62 (cm)

sinB = AC/BC = 12/13

⇒ ∠B ≈ 67⁰

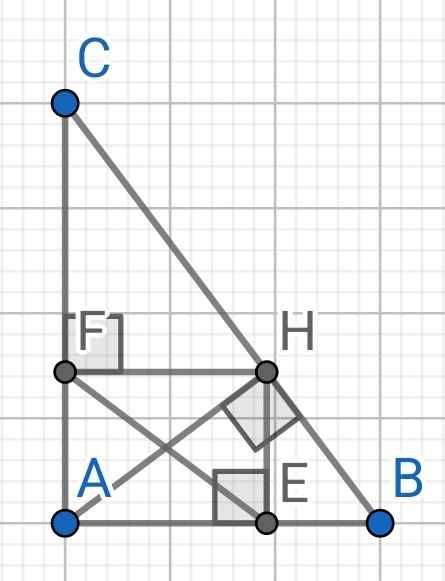
b) ∆AHB vuông tại H có HE là đường cao

⇒ HE² = AE . EB (1)

∆AHC vuông tại H có HF là đường cao

⇒ HF² = AF . FC (2)

Tứ giác AEHF có:

∠AEH = ∠EAF = ∠AFH = 90⁰

⇒ AEHF là hình chữ nhật

⇒ AH = EF

⇒ ∠EHF = 90⁰

∆EHF vuông tại H

⇒ EF² = HE² + HF²

⇒ AH² = HE² + HF²

Từ (1) và (2)

⇒ AE.EB + AF.FC = HE² + HF² = AH²

∆ABC vuông tại A vó AH là đường cao

⇒ AH² = HB.HC

⇒ AE.EB + AF.FC = HB.HC

⇒ AE.EB + AF.FC - HB.HC = 0

c) AH = EF đã chứng minh ở câu b