GDCD CÓ BAO NHIÊU BÀI TỪ L6-9 plS HELP ME
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có:
+các số chi hết cho 3 có 2 chữ số là:12;15;...;99
các số trên cách nhau 3 đơn vị
=> số các số chia hết chỏ có 2 chữ số là:
(99-12)/3+1=30(số)
Các số có 2 chữ số chia hết cho 3 là : 12 ; 15 ; 18 ; 21 ; ... ; 99
Khoảng cách của chúng là : 3 đơn vị
Vậy số số chia hết cho 3 có 2 chữ số là :
\(\frac{99-12}{3}+1=30\)( số )
Vậy số chữ số chia hết cho 3 là :
30 . 2 = 60 ( chữ số )
Đáp số : 60 chữ số

Đổi : m = dm
Hiệu số phần bằng nhau là:
9 - 4 = 5 (phần)
Đường chéo lớn là :
: 5 x 9 = (dm)
Đường chéo bé là :
- = (dm)
Diện tích hình thoi là :
(dm2)

Con chim sáo đang đậu trên cành cây.
Chú thổi sáo này tài quá !
Mik làm theo yêu cầu đó
Con sáo đó hót rất hay
Mọi thứ bị sáo trộn hết cả rồi

Từ \(\text{100 → 199}\) ta dùng 10 chữ số 9 ở hàng đơn vị và 10 chữ số 9 ở hàng chục.
⇒ Từ\(\text{ 100 → 199}\) ta dùng \(\text{20 }\)chữ số \(9\)
⇒ Như vậy ta cần dùng: \(\text{20 x 9 = 180.}\)
Chữ số 9 chưa tính là chữ số 9 ở hàng trăm.
Vậy từ \(\text{900 }\)→ \(\text{999}\) có \(\text{100 }\)chữ số 9 ở hàng trăm.
⇒ Từ \(\text{100 }\)→ \(\text{999}\) ta cần dùng \(\text{100 + 180 = 280 }\)( chữ số 9 )

`7(x-1/2)^2=9`
`(x-1/2)^2=9/7`
\(=>\left[{}\begin{matrix}x-\dfrac{1}{2}=\sqrt{\dfrac{9}{7}}\\x-\dfrac{1}{2}=-\sqrt{\dfrac{9}{7}}\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{3}{\sqrt{7}}+\dfrac{1}{2}\\x=-\dfrac{3}{\sqrt{7}}+\dfrac{1}{2}\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{6+\sqrt{7}}{2\sqrt{7}}\\x=\dfrac{-6+\sqrt{7}}{2\sqrt{7}}\end{matrix}\right.\)
7.(x-\(\dfrac{1}{2}\))2=9
7.x+\(\dfrac{1}{4}\) =9
7.x=\(\dfrac{37}{4}\)
x=\(\dfrac{37}{28}\)


Bài 4:
Ta có: \(\left(4n+3\right)^2-25\)
\(=\left(4n+3-5\right)\left(4n+3+5\right)\)
\(=\left(4n-2\right)\left(4n+8\right)\)
\(=8\left(n+2\right)\left(2n-1\right)⋮8\)
Bài 4:
Ta có: ( 4n + 3 )2 - 25
= ( 4n + 3 - 5 ) . ( 4n + 3 + 5 )
= ( 4n - 2 ) . ( 4n + 8 )
= 8 ( n + 2 ) . ( 2n - 1 ) dấu chia hết 8
Mik ko viết đc dấu chia hết nhé

c: Trường hợp 1: n=2k
\(\Leftrightarrow n\left(n+2017\right)=2k\left(2k+2017\right)⋮2\)
Trường hợp 2: n=2k+1
\(\Leftrightarrow n\left(n+2017\right)=\left(2k+1\right)\left(2k+2018\right)⋮2\)
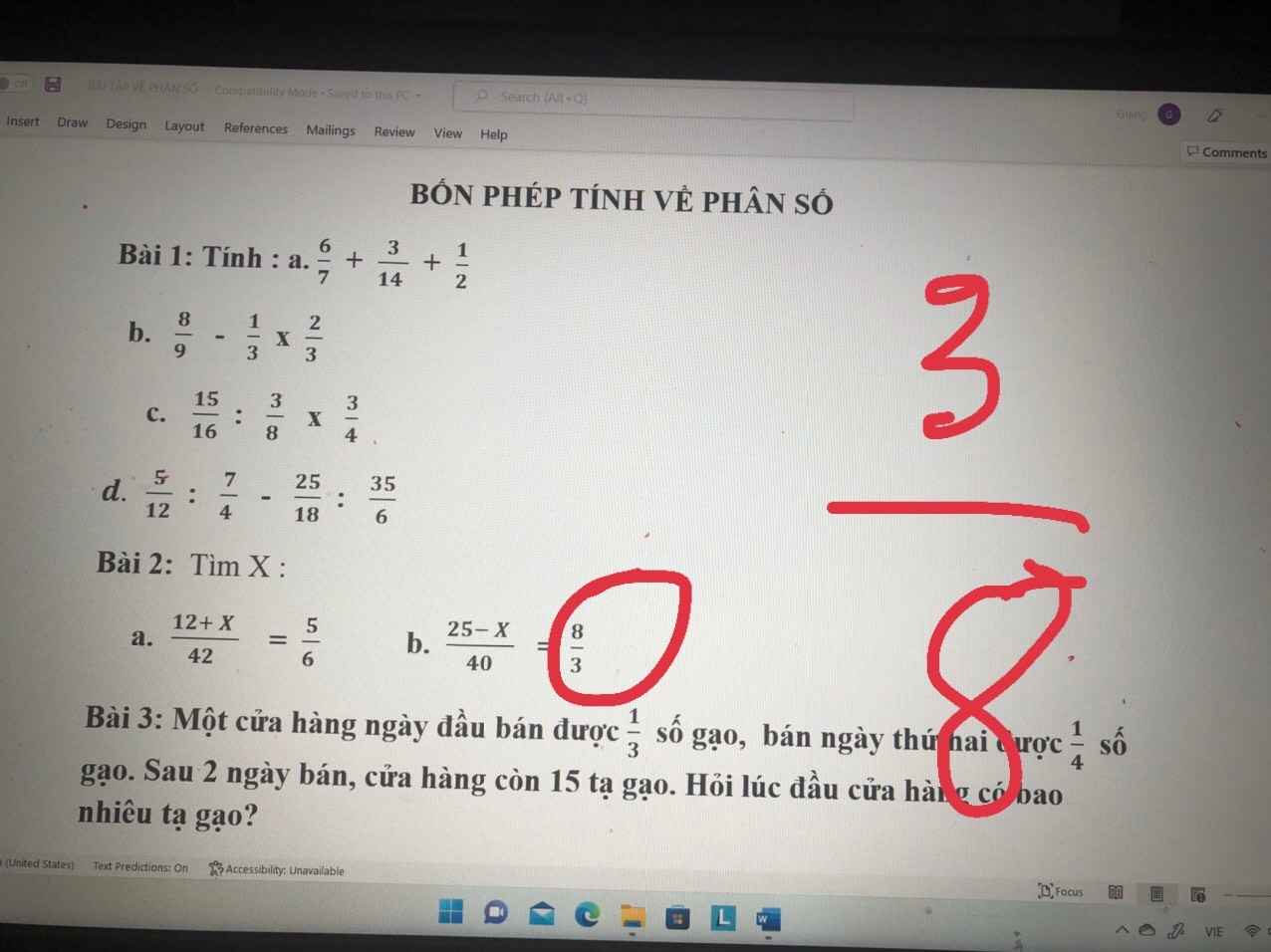

 help me, pls. Sắp đến giờ nộp bài rồi, các bn giúp mình với
help me, pls. Sắp đến giờ nộp bài rồi, các bn giúp mình với
GDCD có 75 bài từ lớp 6 đến lớp 9 nhé.
Chúc bạn học tốt!