Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho tam giác ABC, AB<AC.Tia p/g của góc A cắt BC ở D, trên tia AC lấy điểm E sao cho AE=AB. Gọi tia M là giao điểm của AB va DE
Cmr: a) tam giác ABD=tam giacd AED
b) tam giacd DBM=tam giác DEC
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: DB=DE và \(\widehat{ABD}=\widehat{AED}\)
hay \(\widehat{DBF}=\widehat{DEC}\)
Xét ΔDBF và ΔDEC có
\(\widehat{DBF}=\widehat{DEC}\)
DB=DE
\(\widehat{BDF}=\widehat{EDC}\)
Do đó: ΔDBF=ΔDEC
a: Xét ΔADF và ΔADC có
AD chung
\(\widehat{FAD}=\widehat{CAD}\)
AF=AC
Do đó: ΔADF=ΔADC
b: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE và \(\widehat{ABD}=\widehat{AED}\)
Ta có: \(\widehat{ABD}+\widehat{FBD}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{CED}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AED}\)
nên \(\widehat{FBD}=\widehat{CED}\)
Ta có: AB+BF=AF
AE+EC=AC
mà AB=AE và AF=AC
nên BF=EC
Xét ΔDBF và ΔDEC có
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
BF=EC
Do đó: ΔDBF=ΔDEC
=>\(\widehat{BDF}=\widehat{EDC}\)
mà \(\widehat{EDC}+\widehat{BDE}=180^0\)(hai góc kề bù)
nên \(\widehat{BDE}+\widehat{BDF}=180^0\)
=>E,D,F thẳng hàng
c: Ta có: ΔDBF=ΔDEC
=>DF=DC
=>D nằm trên đường trung trực của CF(1)
ta có: AF=AC
=>A nằm trên đường trung trực của CF(2)
Từ (1) và (2) suy ra AD là đường trung trực của CF
=>AD\(\perp\)CF
a+b) Xét \(\Delta AFE\) và \(\Delta ACB:\)
Ta có:\(A\) là góc chung
AE=AB (gt)
AF=AC (gt)
Vậy \(\Delta AFE=\Delta ACB\)(c.g.c)
Vậy \(AFE=ACB\) góc tương ứng 1
Xét \(\Delta ABD\) và \(\Delta AED\)
Ta có : \(BAD=EAD\) ( gt )
AD là cạnh chung
AB=AE (cạnh tương ứng)
Vậy \(\Delta ABD=\Delta AED\) ( c.g.c)
Vậy BD=ED (cạnh tương ứng ) (2)
Xét \(\Delta BDF\) và \(\Delta EDC\)
Ta có: EC=BF ( Do EA=BA và AC=AF mà EC=AC-EA, BF=AF-AB )
Từ (1)(2)
Vậy \(\Delta BDF=\Delta EDC\) ( c.g.c)
c. Ta có: \(BDF=EDC\) ( góc đối, cm câu a)
Nên F, D, E thẳng hàng
d. AC=AF (cạnh tương ứng, cm trên)
Nên AD là đường phân giác đồng thời đường cao ứng \(\Delta ACF\) cân nên AD vuông góc FC
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE và \(\widehat{ABD}=\widehat{AED}\)
Ta có: \(\widehat{ABD}+\widehat{DBF}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{DEC}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AED}\)
nên \(\widehat{DBF}=\widehat{DEC}\)
Ta có: AB+BF=AF
AE+EC=AC
mà AB=AE và AF=AC
nên BF=EC
Xét ΔDBF và ΔDEC có
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
BF=EC
Do đó: ΔDBF=ΔDEC
b: Ta có: AB+BF=AF
AE+EC=AC
mà AB=AE và AF=AC
nên BF=EC
c: Ta có: ΔDBF=ΔDEC
=>\(\widehat{BDF}=\widehat{EDC}\)
mà \(\widehat{EDC}+\widehat{EDB}=180^0\)
nên \(\widehat{BDF}+\widehat{EDB}=180^0\)
=>E,D,F thẳng hàng
d: ta có: ΔDBF=ΔDEC
=>DF=DC
=>D nằm trên đường trung trực của FC(1)
ta có: AF=AC
=>A nằm trên đường trung trực của CF(2)
Từ (1) và (2) suy ra AD là đường trung trực của CF
=>AD\(\perp\)CF
a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đo: ΔABD=ΔAED
=>DB=DE
Xét ΔDBF và ΔDEC có
góc DBF=góc DEC
DB=DE
góc BDF=góc EDC
Do đó: ΔDBF=ΔDEC
=>BF=EC
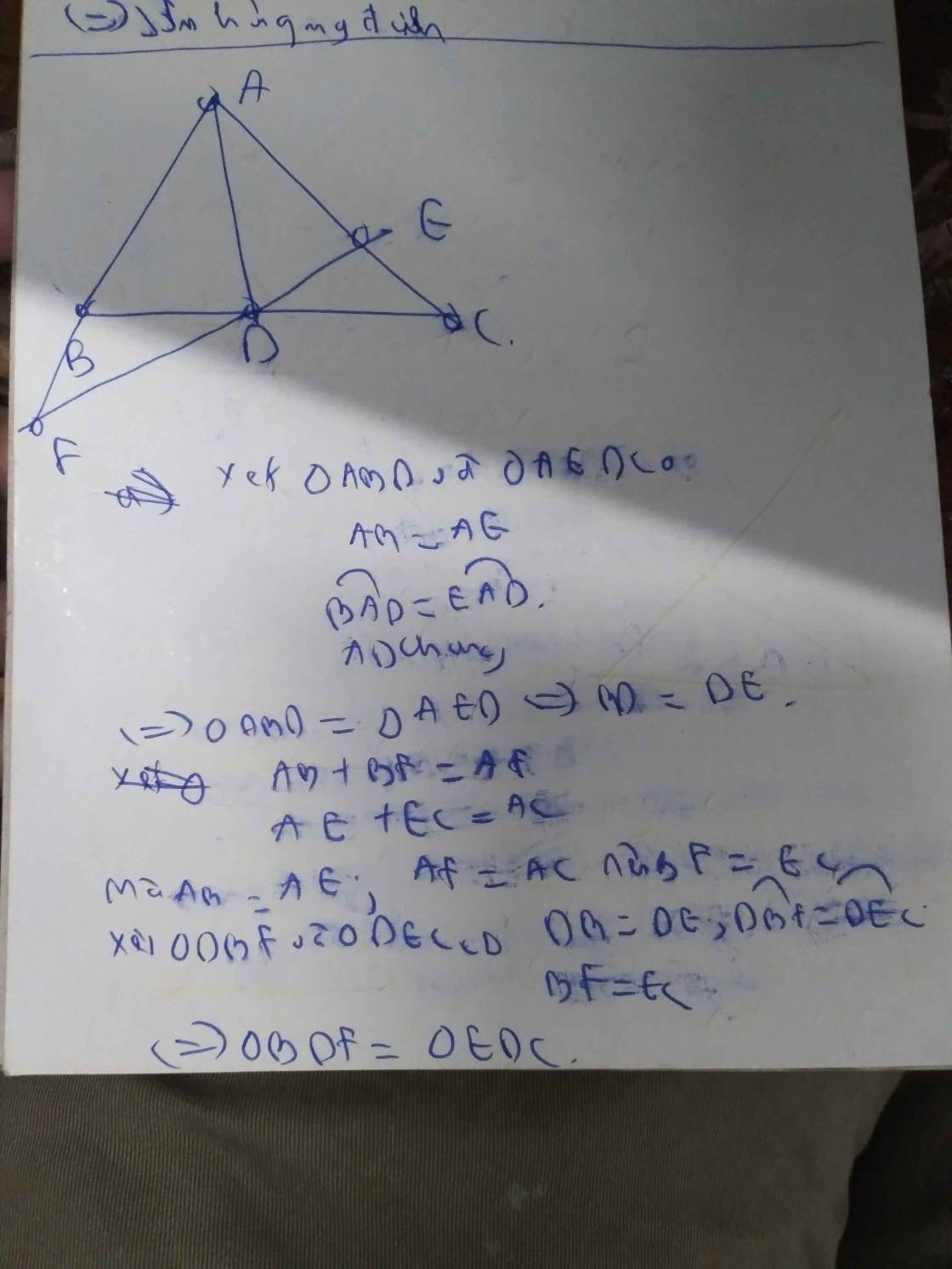
a)Xét tam giác ABD và tam giác AED có:
AB=AE(gt)
góc BAD=góc EAD(do AD là tia phân giác của góc BAC)
AD là cạnh chung
Do đó: tam giác BAD= tam giác EAD(c.g.c)
=> BD=DE( 2 cạnh T.Ư)
Xét tam giác FAD và tam giác CAD có:
FA=CA(gt)
góc BAD=góc EAD(do AD là tia phân giác của góc BAC)
AD là cạnh chung
Do đó tam giác FAD= tam giác CAD(c.g.c)
=> FD=CD( 2 cạnh T.Ư)
Xét tam giác BDF và tam giác EDC có:
BD=DE(CMT)
góc BDF=góc EDC( vì đối đỉnh)
FD=CD( 2 cạnh T.Ư)
Do đó tam giác BDF= tam giác EDC(c.g.c)
Gửi trước câu a
b)
=> BF=EC( 2 cạnh T.Ư)