Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét ΔABH vuông tại H và ΔKIH vuông tại H có
HB=HI(gt)
HA=HK(gt)
Do đó: ΔABH=ΔKIH(Hai cạnh góc vuông)
a: Xét ΔABH vuông tại H và ΔKIH vuông tại H có
HA=HK
HB=HI
=>ΔABH=ΔKIH
b: ΔABH=ΔKIH
=>góc ABH=góc KIH
=>AB//IK
c: IK//AB
AB vuông góc AC
=>IK vuông góc AC
=>I,K,E thẳng hàng
d: Xét tứ giác ABKI có
H là trung điểm chung của AK và BI
AK vuông góc BI
=>ABKI là hình thoi
=>AB=AI=IK
=>IK=ID
=>góc IKD=góc IDK
xét tam giác ABE và tam giác ADE
AE chung
góc BAE = góc DAE(AE la tia phân giác của góc E)
AB = AD ( gt)
=> tam giác ABE = tam giac DAE ( c.g.c)
b) xét tam giác ABI và tam giác ADI
AI chung
góc BAE = góc DAE
tam giác ABI=tam giác ADI
=> BI = DI ( 2 cạnh t/ứ )
=> I là trung điểm của BD
a) xét ΔABH và ΔACH, ta có :
AB = AC (giả thiết)
\(\widehat{ABC}=\widehat{ACB}\) (vì AB = AC => đó là tam giác cân, mà tam giác cân thì có 2 góc ở đáy bằng nhau)
AH là cạnh chung
ð ΔABH = ΔACH (c.c.c)
b) vì ΔABH = ΔACH, nên :
=> HB = HC (2 cạnh tương ứng)
c) hơi khó nha !
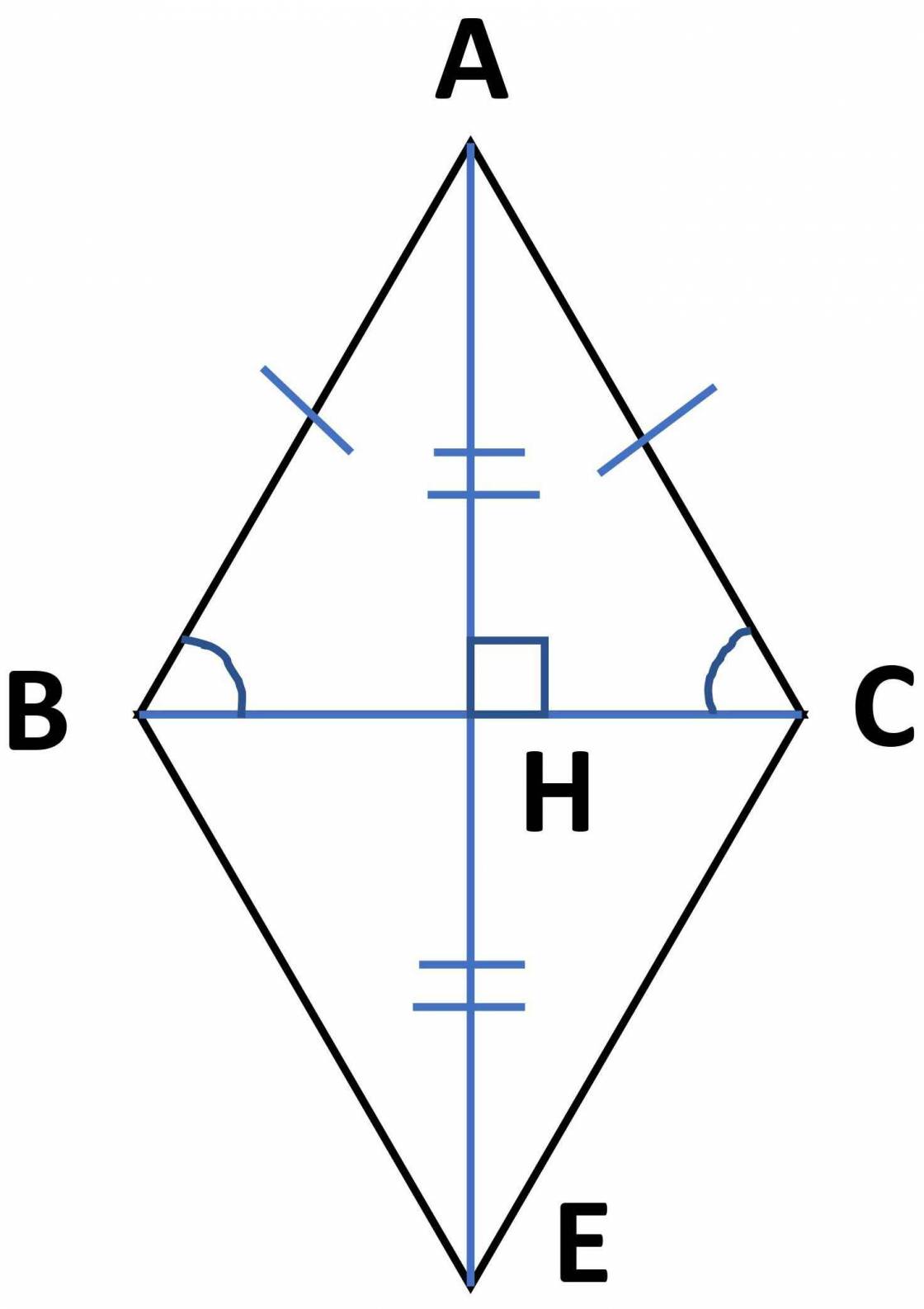
\(a)\)Xét \(\Delta ABH\) và \(\Delta KIH\) có:
\(HA=HK\left(gt\right)\)
\(\widehat{BHA}=\widehat{KHI}\left(đ^2\right)\)
\(HB=HI\left(gt\right)\)
\(\Rightarrow\Delta AHB=\Delta KIH\left(c.g.c\right)\)
\(b)\widehat{BAH}=\widehat{HKI}\left(\Delta AHB=\Delta KIH\right)\)
Mà hai góc ở vị trí so le trong
\(\Rightarrow AB//KI\)
\(c)AB\perp AC\)
\(AB//KI\)
\(\Rightarrow KI\perp AC\)
\(\Rightarrow IE\perp AC\)
\(\Rightarrow IK\equiv IE\)
\(\Rightarrow K,I,E\) thẳng hàng
\(d)\)Sai đề