Gọi độ dài các cạnh của tam giác lần lượt là x, y, z (cm)

Theo đề bài ta có x + y + z = 36 và

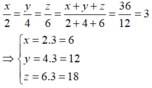
Chọn đáp án B

a: Gọi độ dài ba cạnh lần lượt là a,b,c

Theo đề, ta có: a/4=b/5=c/7 và a+b+c-2a=2

Áp dụng tính chất của DTBSN, ta được:

\(\dfrac{a}{4}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c-2a}{4+5+7-2\cdot4}=\dfrac{2}{8}=\dfrac{1}{4}\)

=>a=1; b=5/4; c=7/4

b: Gọi độ dài ba cạnh lần lượt là a,b,c

Theo đề, ta có:

a/2=b/4=c/5

Áp dụng tính chất của DTSBN, ta đc:

\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{2+4+5}=\dfrac{33}{11}=3\)

=>a=6; b=12; c=15

Tham khảo?

Nhìn là biết.......:)

Gọi hai cạnh góc vuông cần tìm là AB,AC và cạnh huyền là BC(Điều kiện: AB>0; AC>0; BC>0)

Theo đề, ta có: AB:AC=3:4 và AB+AC+BC=24(cm)

⇔\(\dfrac{AB}{AC}=\dfrac{3}{4}\)

\(\Leftrightarrow\dfrac{AB}{3}=\dfrac{AC}{4}\)

Đặt \(\dfrac{AB}{3}=\dfrac{AC}{4}=k\)

\(\Leftrightarrow\left\{{}\begin{matrix}AB=3k\\AC=4k\end{matrix}\right.\)

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(AB^2+AC^2=BC^2\)

\(\Leftrightarrow BC^2=\left(3k\right)^2+\left(4k\right)^2=25k^2\)

hay BC=5k

Ta có: AB+AC+BC=24cm(gt)

\(\Leftrightarrow3k+5k+4k=24\)

\(\Leftrightarrow12k=24\)

hay k=2

⇔AB=6cm; AC=8cm

Vậy: Độ dài hai cạnh góc vuông cần tìm là 6cm và 8cm

Tìm được độ dài các cạnh của tam giác lần lượt là:

6 cm, 8 cm, 10 cm.

Gọi a,b,c là độ dài 3 cạnh của tam giác đó

Theo đề ta có:

\(\dfrac{a}{3}=\dfrac{b}{4}\)

Đặt: \(\dfrac{a}{3}=\dfrac{b}{4}=k\)

\(\Rightarrow\left\{{}\begin{matrix}a=3k\\b=4k\end{matrix}\right.\)

Tam giác vuông. Áp dụng định lí Pitago ta có: 

a² + b² = c²

=> (3k)² + (4k)² = c²

=> 9k² + 16k² = c²

=> 25k² = c²

=> c = 5k

Theo đề ta có:

a + b + c = 24

=> 3k + 4k + 5k = 24

=> 12k = 24

=> k = 2

Mà: \(\left\{{}\begin{matrix}a=3k\\b=4k\\c=5k\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a=3.2=6\left(cm\right)\\b=4.2=8\left(cm\right)\\c=5.2=10\left(cm\right)\end{matrix}\right.\)

Vậy: Độ dài 3 cạnh của tam giác đó là 6, 8, 10

Gọi độ dài ba cạnh của tam giác theo thứ tự từ nhỏ đến lớn là x,y,z (tính bằng m)

(x > 0; y > 0 và z > 6)

* Cạnh lớn nhất dài hơn cạnh nhỏ nhất là 6m nên: z - x = 6

Vì 3 cạnh của tam giác tỉ lệ với 3,4,5 nên ta có:

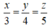
Theo tính chất dãy tỉ số bằng nhau ta có:

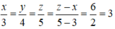
x/3 = 3 ⇒ x = 3.3 = 9

y/4 = 3 ⇒ y = 4.3 = 12

z/5 = 3 ⇒ z = 5.3 = 15

Vậy độ dài 3 cạnh của tam giác là 9m; 12m; 15m

Gọi độ dài 3 cạnh tam giác lần lượt là x;y;z

Do độ dài các cạnh tỉ lệ với 3;5;7 nên: \(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}\)

Do cạnh lớn nhất dài hơn cạnh nhỏ nhất 40m nên: \(z-x=40\)

Áp dụng tính chất tỉ lệ thức:

\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{z-x}{7-3}=\dfrac{40}{4}=10\)

\(\Rightarrow\left\{{}\begin{matrix}x=3.10=30\\y=5.10=50\\z=7.10=70\end{matrix}\right.\)

Vậy độ dài 3 cạnh tam giác là 30m, 50m, 70m

tôi đăng câu hỏi lên để hỏi nếu mà biết tôi đã tự làm rồi

Gọi độ dài các cạnh của tam giác đó là a,b,c (a,b,c thuộc tập hợp Q)

Do các cạnh của tam giác đó tỉ lệ với 2;4;5 nên 

\(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}\)và a+b+c=22 cm

Áp dụng tính chất của dãy tỉ số bằng nhau ta có

\(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}=\frac{a}{2}+\frac{b}{4}+\frac{c}{5}=\frac{22}{11}=2\)

Do đó

\(\frac{a}{2}=2\Rightarrow a=4cm\)

\(\frac{b}{4}=2\Rightarrow b=8cm\)

\(\frac{c}{5}=2\Rightarrow c=10cm\)

Vậy độ dài các cạnh của tam giác đó lần lượt là 4;8;10 cm

Gọi độ dài các cạnh của 1 tam giác lần lượt là: x, y , z.

Ta có:

Độ dài các cạnh của tam giác tỉ lệ với các số 2;4;5 => x/2=y/4=z/5

x+y+z=22

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

x/2=y/4=z/5=x+y+z/2+4+5=22/11=2

x=4; y=8; z=10