Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1:Gọi giao của DO và CB là H
Xét ΔOAD vuông tại A và ΔOBH vuông tại B có
OA=OB
góc AOD=góc BOH
=>ΔOAD=ΔOBH
=>OD=OH
=>ΔCDH cân tại C
=>ΔAOD đồng dạng với ΔBOH
Xét ΔBOH vuông tại B và ΔOCH vuông tại O có
góc BHO chung
=>ΔBOH đồng dang với ΔOCH
=>ΔAOD đồng dạng với ΔOCH
2: ΔCHD cân tại C
=>góc CDH=góc CHD=góc ADH
=>DH là phân giác của góc ADC
*Độc giả tự vẽ hình, người giải ko biết cách đăng hình:))*
Gọi giao điểm của CO và BD là Z
Xét 2 tam giác vuông AOC và BOZ có:
OA=OB (O là trung điểm AB)
Góc AOC = góc BOZ (đối đỉnh)
Suy ra: tam giác AOC = tam giác BOZ (cgv-gn)
Do đó: AC=BZ và OC=OZ (các cặp cạnh tương ứng)
Vì OC=OZ nên O là trung điểm CZ => OD là đường trung tuyến tam giác DCZ (1)
Vì OD vuông góc OC nên OD là đường cao tam giác DCZ (2)
Từ (1) và (2) suy ra: tam giác DCZ cân tại D (có OD vừa là đường cao vừa là đường trung tuyến) => CD=DZ (3)
Mặt khác: DZ=BD+BZ
Mà: AC=BZ (cmt)
Nên: DZ=BD+AC (4)
Từ (3) và (4) suy ra: CD=BD+AC (đpcm)
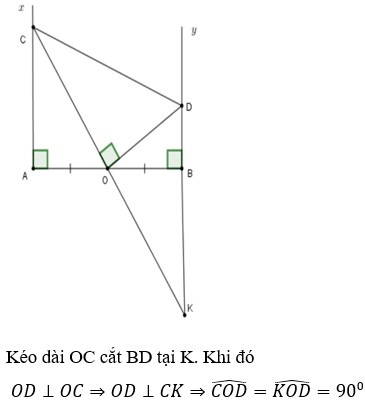
a, xét tgACO và tgBEO có: gCAO=gEBO = 90 độ
OA=OB (O là trung điểm của AB)
gAOC = gBOE (hai góc đối đỉnh)
=>tgACO=tgEBO(g.c.g)=>AC=BE;OC=OE (hai cạnh tương ứng)
xét tgCOD và tgEOD có: OC=OE (cmt)
gCOD=gEOD=90độ
OD là cạnh chung
=>tgCOD=tgEOD (c.g.c)
=> CD= DE (hai cạnh tương ứng)
mà DE=DB+BE =>CD=DB+BE
mà BE=AC(cmt)=>CD=AC+BD
b, xét tgCOJ và tgEOJ có : OC=OE (cmt)
gCOJ=gEOJ = 90độ
OJ là cạnh chung
=>tgCOJ=tgEOJ (c.g.c)=>gJCO=gJEO;JC=JE
xét tgCDJ và tgEDJ có: CD=DE (cmt)
DJ là cạnh chung
CJ=EJ (cmt)
=>tgCDJ=tgEDJ (c.c.c)
=>gDCJ=gDEJ
mà gDCJ = gJCO (CJ là tia phân giác của gOCD)
gJCO=gJEO (cmt)
=>gDEJ = gJEO =>EJ là tia phân giác của gBEO