Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét ΔDAB và ΔDEB có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔDAB=ΔDEB(c-g-c)
Suy ra: DA=DE(Hai cạnh tương ứng)
a: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
c: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
DO đó: ΔADK=ΔEDC
Suy ra: DK=DC
hay ΔDKC cân tạiD
tự vẽ hình giúp mình nha ^^
áp dụng định lí py-ta-go vào tam giác vuông ABC
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2\)
\(\Leftrightarrow AC^2=10^2-6^2=100-36=64\)
\(\Rightarrow AC=\sqrt{64}=8\left(cm\right)\)
b) Xét \(\Delta BADvà\Delta BEDcó\)
BD:chung
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
AB=BE(gt)
\(\Delta BAD=\Delta BED\left(c-g-c\right)\)
=>DA=DE
c)Xét \(\Delta KADvà\Delta CEDcó\)
\(\widehat{KAD}=\widehat{CED}\left(=90^0\right)\)
\(\widehat{KDA}=\widehat{CDE}\) (đối đỉnh)
\(=>\Delta KAD=\Delta CED\left(g-c-g\right)\)
=>DC=DK
=> tam giác KDC cân tại D
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: DK=DC
hay ΔDKC cân tại D
c: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
d: Ta có: DK=DC
mà DC>DE
nên DK>DE
a: AC=8cm
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
c: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: DK=DC
hay ΔDKC cân tại D
c) Δ ABK = Δ ADK (câu b) => BK = DK (2 cạnh tương ứng)
và ABK = ADK (2 góc tương ứng)
Mà ABK + KBE = 180o (kề bù)
ADK + KDC = 180o (kề bù)
nên KBE = KDC
Xét Δ KBE và Δ KDC có:
BE = CD (gt)
KBE = KDC (cmt)
BK = DK (cmt)
Do đó, Δ KBE = Δ KDC (c.g.c)
=> BKE = DKC (2 góc tương ứng)
Lại có: BKD + DKC = 180o (kề bù)
Do đó, BKE + BKD = 180o
=> EKD = 180o
hay 3 điểm E, K, D thẳng hàng (đpcm)
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b, Ta có : góc BAD = góc BED=90 độ (hai góc tương ứng)
=> góc BED là góc V
Ta có ; DA=DE (hai cạnh tương ứng)
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó:ΔADK=ΔEDC
Suy ra:DK=DC
hay ΔDKC cân tại D
c: BC=10cm
AB=6cm
=>AC=8cm
a) Xét tam giác ABD và tam giác EBD có:
+ ^ABD = ^EBD (do BD là phân giác ^B).
+ BD chung.
+ AB = BE (gt).
=> Tam giác ABD = Tam giác EBD (c - g - c).
=> DA = DE (2 cạnh tương ứng).
b) Tam giác ABD = Tam giác EBD (cmt).
=> ^BAD = ^BED (2 góc tương ứng).
Mà ^BAD = 90o (gt).
=> ^BED = 90o.
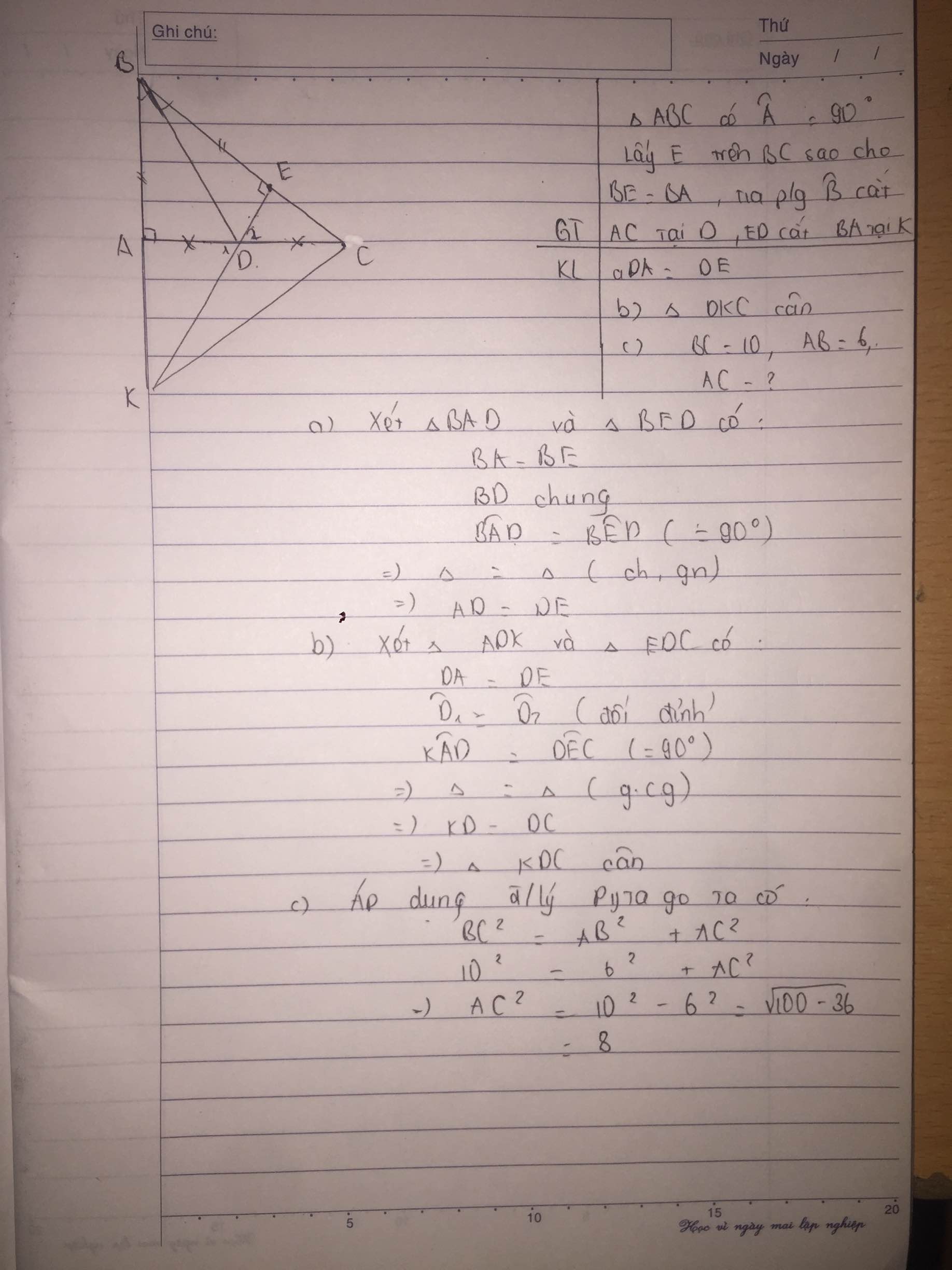
a, Xét tg ABD và tg EBD có : AB = EB (gt)
gABD = gEBD (BD là tia phân giác của gABE)
BD chung
=> tgABD = tgEBD (c.g.c)
=> DA = DE ( hai cạnh tương ứng )
b,vì tgABD = tgEBD (cmt)
=>gABD = gAEB=90 độ (hai góc tương ứng)
=>gDAK = gDEC = 90 độ
xét tgAKD và tgEDC có: gDAK = gDEC (cmt)
AD = DE ( cmt)
gADK = gEDC ( hai góc đối đỉnh)
=> tgAKD = tgEDC (g.c.g)
=> DK = DC (hai cạnh tương ứng)
=> tg DKC cân tại D
c,xét tgABC vuông tại A ( góc A = 90độ , theo định lí Pytago ta có
BC^2=AB^2 + AC^2
=>AC^2 = 100- 36=64
=> AC = 8 (cm)
a, xét tam giác ABD và tam giác EBD có : BD chung
BA = BE (Gt)
góc ABD = góc EBD do BD là phân giác của góc ABC (gt)
=> tam giác ABD = tam giác EBD (c-g-c)
=> AD = DE (đn)
b, Xét tam giác DCE và tam giác KDA có : AD = DE (Câu a)
góc KDA = góc CDE (đối đỉnh)
góc CED = góc DAK = 90
=> tam giác CE = KA (đn)
có AB = BE (gt)
AB + KA = BK
BE + EC = BC
=> BC = BK
=> BCK cân tại B (đn)
c, dùng ty ta go thôi