Tìm các số nguyên x,y sao cho: (x-13).(y+2)=13
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a) x . y = 13 nên x ∈ U 13 và y ∈ U 13 do đó ta có x ; y ∈ 1 ; 13 ; 1 3 ; 1 ; − 1 ; − 13 ; − 13 ; − 1
b) x . y = 8 và x < y ; x ∈ U 8 ; y ∈ U 8 do đó ta có x ; y ∈ − 8 ; − 1 ; − 4 ; − 2 ; 1 ; 8 ; 2 ; 4

a) x . y = 13 nên x ∈ U 13 và y ∈ U 13 do đó ta có x ; y ∈ 1 ; 13 ; 1 3 ; 1 ; − 1 ; − 13 ; − 13 ; − 1
b) x . y = 8 v à x < y , x ∈ U 8 , y ∈ U 8 do đó ta có x ; y ∈ − 8 ; − 1 ; − 4 ; − 2 ; 1 ; 8 ; 2 ; 4

\(x^2=\left(y+1\right)^2+12\)
\(\Leftrightarrow\left(x-y-1\right)\left(x+y+1\right)=12\)
Do \(x,y\in N\)* nên \(x-y-1;x+y+1\inƯ\left(12\right)\) và \(x+y+1\ge1+1+1=3\)
TH1: \(x+y+1=12\Rightarrow x-y-1=1\)
\(\Leftrightarrow x=\dfrac{13}{2};y=\dfrac{9}{2}\) (ktm)
TH2:\(x+y+1=6;x-y-1=2\)
\(\Leftrightarrow x=4;y=1\) (thỏa mãn)
TH3: \(x+y+1=4;x-y-1=3\)
\(\Leftrightarrow x=\dfrac{7}{2};y=-\dfrac{1}{2}\) (ktm)
TH4: \(x+y+1=3;x-y-1=4\) (ktm)
Vậy \(x=4;y=1\)
\(x^2=y^2+2y+13\)
\(\Leftrightarrow x^2=y^2+2y+1+12\)
\(\Leftrightarrow x^2=\left(y+1\right)^2+12\)
\(\Leftrightarrow x^2-\left(y+1\right)^2=12\)
\(\Leftrightarrow\left(x-y-1\right)\left(x+y+1\right)=12\)
Vi x;y nguyên dương
\(\Rightarrow\left(x-y-1\right);\left(x+y+1\right)\in B\left(12\right)=\left\{1;2;3;4;6;12\right\}\left(x-y-1< x+y+1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x+y+1\in\left\{12;6;4\right\}\\x-y-1\in\left\{1;2;3\right\}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x\in\left\{\dfrac{13}{2};4;\dfrac{7}{2}\right\}\\y\in\left\{\dfrac{9}{2};1;-\dfrac{1}{2}\right\}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=4\\y=1\end{matrix}\right.\) (x;y nguyên dương)
Vậy \(\left(x;y\right)\in\left(4;1\right)\) thỏa mãn đề bài

2,
-Ta có: \(x^2+45=y^2\)
\(\Leftrightarrow y^2>45\Rightarrow y\) là số ng tố lẻ
\(\Rightarrow x^2\)chẵn( vì: chẵn +5=lẻ)
\(\Rightarrow x=2\)
\(\Leftrightarrow2^2+45=y\)
\(\Leftrightarrow y=\pm\sqrt{49}=\pm7\)
-Mà: snt>0
-Vậy: \(x=2;y=7\)
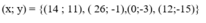
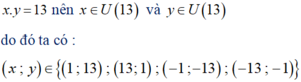
Vì \(x,y\inℤ\) và \(\left(x-13\right)\cdot\left(y+2\right)=13\Rightarrow y+2\inƯ\left(13\right)=\left\{\pm1;\pm13\right\}\)
x-13
(x-13).(y+2)=13
=> (y+2)\(\in\)Ư(13)={1;13; -13; -1}
Nếu y+2= 1 => x= 1-2 => y= -1
Nếu y+2=13 => y= 13-2 => y= 11
Nếu y+2= -1 => y= -1-2 => y= -3
Nếu y+2 = -13 => y= -13-2 => y= -15
Sau đó bn thay vào r tự tìm nha