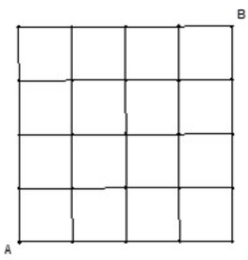
Hình dưới đây biểu diễn phần trên cùng bên trái của bảng lưới 101 × 101 ô vuông trắng. Người ta tô màu xám cho một số ô vuông để tạo thành một "dây" ô vuông. Dây này bắt đầu từ ô vuông góc trên cùng bên trái và tiếp tục cho đến khi không thể kéo dài được nữa. Hỏi trong bảng lưới 101 × 101 có bao nhiêu ô vuông được tô màu xám?




Lấy đỉnh trên cùng bên trái của bảng lưới 101 × 101 làm mốc cố định.
Xét dãy các bảng lưới hình vuông có cạnh tăng dần 1, 2, 3, ... 100, 101 cùng chứa mốc đã chọn. Để ý rằng các bảng lưới có cạnh chẵn luôn chứa số ô vuông xám bằng số ô vuông trắng.
Suy ra số ô vuông xám trong bảng lưới 100 × 100 là: 50 × 100 = 5000 (ô).
Mặt khác, trong 2 bảng lưới hình vuông liên tiếp cạnh (2n) và (2n + 1), số ô vuông xám được tăng thêm sẽ là (1 + 4n). Như vậy, chênh lệch số ô vuông xám trong bảng lưới 101 × 101 với bảng lưới 100 × 100 là: 1 + 4 × 50 = 201 (ô).
Vậy số ô vuông xám trong bảng lưới 101 × 101 là: 5000 + 201 = 5201.
Đáp số: 5201 ô vuông xám
học tốt