cho tam giác ABC có gócB= gócC .tia phân giác của góc A cắt BC tại D.CMR:a) tam giác ADB = tam giác ADC b) AB = AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét \(\Delta ABD\)và \(\Delta ADC\)có:
\(\widehat{B}=\widehat{C}\left(gt\right)\)
AD là cạnh chung
\(\widehat{A_1}=\widehat{A_2}\)( do AD là tia phân giác góc A )
\(\Rightarrow\Delta ABD=\Delta ADC\left(g.c.g\right)\)
b) Vì \(\widehat{B}=\widehat{C}\left(gt\right)\)
\(\Rightarrow\Delta ABC\)cân tại A
Vì \(\Delta ABC\)cân tại A
\(\Rightarrow AB=AC\)( tính chất tam giác cân )
BẠN TỰ VẼ HÌNH NHÉ
a, Ta có: AD là tia phân giác của góc BAC(gt)
=> Góc BAD = Góc DAC = Góc BAC : 2
Xét tam giác BAD và tam giác DAC có góc B + góc BAD + góc BDA = góc C + góc DAC + góc ADC = 180 độ ( ĐL tổng 3 góc của tam giác )
mà góc B = góc C (gt) và góc BAD = góc DAC (cmt)
=> góc BDA = góc ADC
Xét tam giác ADB và tam giác ADC có:
Góc DAB = Góc DAC (cmt)
AD CHUNG
Và góc ADB = góc ADC (cmt)
=> Tam giác ADB = Tam giác ADC (g-c-g)
b, Từ tam giác ADB = tam giác ADC (cmt) => AB = AC ( 2 cạnh tương ứng của 2 tam giác bằng nhau )

b ) GÓC B = GÓC C
=> TAM GIÁC ABC CÂN TẠI A
=> AB = AC (ĐPCM)
a) XÉT 2 TAM GIÁC ADB VÀ ADC, CÓ:
AB = AC (THEO CÂU B)
AD LÀ CẠNH CHUNG
GÓC A1 = GÓC A2 (AD LÀ PHÂN GIÁC, GT)
=> TAM GIÁC ADB = ADC (C.G.C) (ĐPCM)
a) Xét tam giác adb và tam giác adc
ab = ac
góc a1 và góc a2 là cạnh chung
Suy ra tam giác adb = tam giác adc
b) Vì tam giác adb = tam giác adc
Nên AB = AC

b ) GÓC B = GÓC C
=> TAM GIÁC ABC CÂN TẠI A
=> AB = AC (ĐPCM)
a) XÉT 2 TAM GIÁC ADB VÀ ADC, CÓ:
AB = AC (THEO CÂU B)
AD LÀ CẠNH CHUNG
GÓC A1 = GÓC A2 (AD LÀ PHÂN GIÁC, GT)
=> TAM GIÁC ADB = ADC (C.G.C) (ĐPCM)

Tam giác ACD và tam giác ABD có :
Góc B = góc C ( gt )
AD là cạnh chung
Góc A1 = Góc A2 ( AD là tia phân giác của tam giác ABC )
=> tam giác ACD = tam giác ABD
b) Tam giác ABC cân tại A ( góc B = góc C )
=> AB = AC
- SKT_Twisted Fate Âm Phủ
- Sai rồi
- giả thiết cho góc A = góc B chứ đâu cho Góc B = goc C
- Sai rùi
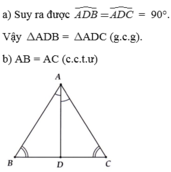
Hình dễ : bn cs thể tự vẽ nha !
a, Xét \(\Delta\)ADB và \(\Delta\)ADC ta cs
AB = AC ( gt )
^A1 = ^A2 ( AD là t p/g của A )
AD_chug
=> \(\Delta\)ADB = \(\Delta\)ADC (c.g.c)
b, Vì \(\Delta\)ADB = \(\Delta\)ADC
=> AB = AC
a, Ta có: góc B = góc C (gt)
=> Tam giác ABC cân tại A
=> AB = AC
Xét tam giác ADB và tam giác ADC có: AB = AC
AD là cạnh chung
Góc BAD = góc CAD
=> Tam giác ADB = tam giác ADC (c.g.c)
b, Ta có: tam giác ABC cân tại A (phần a)
=> AB = AC