Ta có: \(\left(x-1\right)^2+\left(x+y\right)^2\le9\Rightarrow x+y\le3\).

Áp dụng bất đẳng thức AM - GM ta có:

\(\dfrac{2}{x}+2x\ge2\sqrt{\dfrac{2}{x}.2x}=4;\dfrac{4}{y}+y\ge2\sqrt{\dfrac{4}{y}.y}=4\).

Do đó \(\dfrac{2}{x}\ge4-2x;\dfrac{4}{y}\ge4-y\)

\(\Rightarrow P\ge8-4\left(x+y\right)\ge-4\). (do \(x+y\le3\)).

Vậy...

Đẳng thức xảy ra khi và chỉ khi x = 1; y = 2.

Đỉnh cao pạn ưi

Bài 3 :

\(\dfrac{1}{2!}+\dfrac{1}{3!}+\dfrac{1}{4!}+...+\dfrac{1}{2023!}\)

\(\dfrac{1}{2!}=\dfrac{1}{2.1}=1-\dfrac{1}{2}< 1\)

\(\dfrac{1}{3!}=\dfrac{1}{3.2.1}=1-\dfrac{1}{2}-\dfrac{1}{3}< 1\)

\(\dfrac{1}{4!}=\dfrac{1}{4.3.2.1}< \dfrac{1}{3!}< \dfrac{1}{2!}< 1\)

.....

\(\)\(\dfrac{1}{2023!}=\dfrac{1}{2023.2022....2.1}< \dfrac{1}{2022!}< ...< \dfrac{1}{2!}< 1\)

\(\Rightarrow\dfrac{1}{2!}+\dfrac{1}{3!}+\dfrac{1}{4!}+...+\dfrac{1}{2023!}< 1\)

Bạn xem lại đề 2, phần mẫu của N

còn cách làm khác không ạ?

1) Áp dụng bđt Cauchy cho 3 số dương ta có

 \(\dfrac{1}{x}+\dfrac{1}{x}+\dfrac{1}{x}+x^3\ge4\sqrt[4]{\dfrac{1}{x}.\dfrac{1}{x}.\dfrac{1}{x}.x^3}=4\) (1)

\(\dfrac{3}{y^2}+y^2\ge2\sqrt{\dfrac{3}{y^2}.y^2}=2\sqrt{3}\) (2)

\(\dfrac{3}{z^3}+z=\dfrac{3}{z^3}+\dfrac{z}{3}+\dfrac{z}{3}+\dfrac{z}{3}\ge4\sqrt[4]{\dfrac{3}{z^3}.\dfrac{z}{3}.\dfrac{z}{3}.\dfrac{z}{3}}=4\sqrt{3}\) (3)

Cộng (1);(2);(3) theo vế ta được

\(\left(\dfrac{3}{x}+\dfrac{3}{y^2}+\dfrac{3}{z^3}\right)+\left(x^3+y^2+z\right)\ge4+2\sqrt{3}+4\sqrt{3}\)

\(\Leftrightarrow3\left(\dfrac{1}{x}+\dfrac{1}{y^2}+\dfrac{1}{z^3}\right)\ge3+4\sqrt{3}\)

\(\Leftrightarrow P\ge\dfrac{3+4\sqrt{3}}{3}\)

Dấu "=" xảy ra <=> \(\left\{{}\begin{matrix}\dfrac{1}{x}=x^3\\\dfrac{3}{y^2}=y^2\\\dfrac{3}{z^3}=\dfrac{z}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\sqrt[4]{3}\\z=\sqrt{3}\end{matrix}\right.\) (thỏa mãn giả thiết ban đầu)

2) Ta có \(4\sqrt{ab}=2.\sqrt{a}.2\sqrt{b}\le a+4b\)

Dấu"=" khi a = 4b

nên \(\dfrac{8}{7a+4b+4\sqrt{ab}}\ge\dfrac{8}{7a+4b+a+4b}=\dfrac{1}{a+b}\)

Khi đó \(P\ge\dfrac{1}{a+b}-\dfrac{1}{\sqrt{a+b}}+\sqrt{a+b}\)

Đặt \(\sqrt{a+b}=t>0\) ta được

\(P\ge\dfrac{1}{t^2}-\dfrac{1}{t}+t=\left(\dfrac{1}{t^2}-\dfrac{2}{t}+1\right)+\dfrac{1}{t}+t-1\)

\(=\left(\dfrac{1}{t}-1\right)^2+\dfrac{1}{t}+t-1\)

Có \(\dfrac{1}{t}+t\ge2\sqrt{\dfrac{1}{t}.t}=2\) (BĐT Cauchy cho 2 số dương)

nên \(P=\left(\dfrac{1}{t}-1\right)^2+\dfrac{1}{t}+t-1\ge\left(\dfrac{1}{t}-1\right)^2+1\ge1\)

Dấu "=" xảy ra <=> \(\left\{{}\begin{matrix}\dfrac{1}{t}-1=0\\t=\dfrac{1}{t}\end{matrix}\right.\Leftrightarrow t=1\)(tm)

khi đó a + b = 1

mà a = 4b nên \(a=\dfrac{4}{5};b=\dfrac{1}{5}\)

Vậy MinP = 1 khi \(a=\dfrac{4}{5};b=\dfrac{1}{5}\)

Đặt \(\dfrac{x}{y}+\dfrac{y}{x}=t\Rightarrow\left|t\right|\ge2\)

\(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}=t^2-2\)

\(\dfrac{x^4}{y^4}+\dfrac{y^4}{x^4}=\left(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\right)^2-2=\left(t^2-2\right)^2-2=t^4-4t^2+2\)

\(\Rightarrow P=f\left(t\right)=t^4-4t^2+2-\left(t^2-2\right)+t\)

\(f\left(t\right)=t^4-5t^2+t+4\)

Xét hàm \(f\left(t\right)=t^4-5t^2+t+4\) trên \((-\infty;-2]\cup[2;+\infty)\)

\(f'\left(t\right)=g\left(t\right)=4t^3-10t+1\)

\(g\left(t\right)\) bậc 3 nên có tối đa 3 nghiệm

\(g\left(-2\right)=-11\) ; \(g\left(0\right)=1\)

\(\Rightarrow g\left(-2\right).g\left(0\right)< 0\Rightarrow g\left(t\right)=0\) có nghiệm \(t_1\in\left(-2;0\right)\)

\(g\left(1\right)=-5< 0\Rightarrow g\left(0\right).g\left(1\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_2\in\left(0;1\right)\)

\(g\left(2\right)=13\Rightarrow g\left(1\right).g\left(2\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_3\in\left(1;2\right)\)

Dấu \(f'\left(t\right)\):

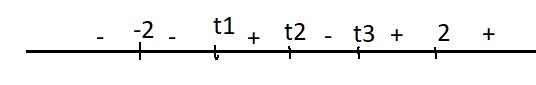
Từ đây ta thấy \(f\left(t\right)\) nghịch biến trên \((-\infty;-2]\) và đồng biến trên \([2;+\infty)\)

Hay GTNN của \(f\left(t\right)\) sẽ rơi vào \(t=-2\) hoặc \(t=2\)

\(f\left(-2\right)=-2\) ; \(f\left(2\right)=2\)

\(\Rightarrow f\left(t\right)_{min}=-2\) khi \(t=-2\) hay \(P_{min}=-2\) khi \(x=-y\)

Lời giải:

$A=(x-y)+\frac{4}{x-y}+y+\frac{1}{y}$

Áp dụng BĐT Cô-si:

$(x-y)+\frac{4}{x-y}\geq 2\sqrt{(x-y).\frac{4}{x-y}}=4$
$y+\frac{1}{y}\geq 2$

$\Rightarrow A\geq 4+2=6$

Vậy $A_{\min}=6$ khi $(x,y)=(3,1)$

\(y=x+\dfrac{1}{x}-5\ge2\sqrt{\dfrac{x}{x}}-5=-3\)

\(y_{min}=-3\) khi \(x=1\)

\(y=4x^2+\dfrac{1}{2x}+\dfrac{1}{2x}-4\ge3\sqrt[3]{\dfrac{4x^2}{2x.2x}}-4=-1\)

\(y_{min}=-1\) khi \(x=\dfrac{1}{2}\)

\(y=x+\dfrac{4}{x}\Rightarrow y'=1-\dfrac{4}{x^2}=0\Rightarrow x=-2\)

\(y\left(-2\right)=-4\Rightarrow\max\limits_{x>0}y=-4\) khi \(x=-2\)

\(A^2=\dfrac{x^2}{y}+\dfrac{y^2}{z}+\dfrac{z^2}{x}+2\left(\dfrac{xy}{\sqrt{yz}}+\dfrac{yz}{\sqrt{xz}}+\dfrac{xz}{\sqrt{xy}}\right)\)

Áp dụng BĐT cosi:

\(\dfrac{x^2}{y}+\dfrac{xy}{\sqrt{yz}}+\dfrac{xy}{\sqrt{yz}}+z\ge4\sqrt[4]{\dfrac{x^4y^2z}{y^2z}}=4x\)

\(\dfrac{y^2}{z}+\dfrac{yz}{\sqrt{xz}}+\dfrac{yz}{\sqrt{xz}}+x\ge4\sqrt[4]{\dfrac{y^4z^2x}{z^2x}}=4y\)

\(\dfrac{z^2}{x}+\dfrac{xz}{\sqrt{xy}}+\dfrac{xz}{\sqrt{xy}}+y\ge4\sqrt[4]{\dfrac{z^4x^2y}{x^2z}}=4z\)

Cộng VTV 3 BĐT trên:

\(\Leftrightarrow A^2+\left(x+y+z\right)\ge4\left(x+y+z\right)\\ \Leftrightarrow A^2\ge3\left(x+y+z\right)\ge3\cdot12=36\\ \Leftrightarrow A\ge6\)

Dấu \("="\Leftrightarrow x=y=z=\dfrac{12}{3}=4\)