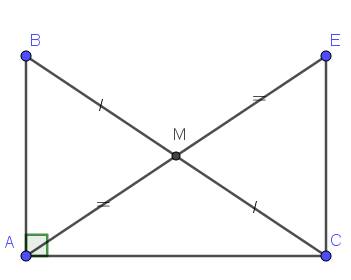
Cho tam giác ABC vuông ở A. Gọi M là trung điểm của BC. Trên tia đối của MA lấy điểm E sao cho ME=MA
a, Tính góc ABC biết góc ACB có số đo bằng 40o
b, CM: tam giác AMB bằng tam giác EMC
CM: AB //EC
c, qua C kẻ đường thẳng d song song với AE, kẻ EK vuông góc vs d tại K
CM: góc KEC bằng góc BCA
(giúp mình nhé a;b rễ rồi chủ yếu là cái phần 'c' ý)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn gõ thừa chữ "cân"
a/ Xét t/g ABC vuông tại A có
\(\widehat{ABC}+\widehat{ACB}=90^o\) (t/c)
\(\Rightarrow\widehat{ABC}=90^o-40^o=50^o\)
b/ Xét t/g AMB và t/g EMC có
AM = EM
\(\widehat{AMB}=\widehat{EMC}\) (đối đỉnh)MB = MC
=> t/g AMB = t/g EMC (c.g.c)c/ Có
AE // CK
=> \(\widehat{AEK}+\widehat{EKC}=180^o\) (tcp)
=> \(\widehat{AEK}=\widehat{AEC}+\widehat{CEK}=90^o\)
Xét t/g ABC vuông tại A có AM là đường trung tuyến
=> AM = 1/2 BC = BM
=> t/g AMB cân tại A
=> \(\widehat{ABC}=\widehat{BAM}\)
Mà \(\widehat{BAM}=\widehat{CEA}\)
=> \(\widehat{CBA}+\widehat{CEK}=90^o\)
=> \(\widehat{CEK}=\widehat{ACB}\)

Lời giải:
a.
Xét tam giác $AMB$ và $EMC$ có:
$\widehat{AMB}=\widehat{EMC}$ (đối đỉnh)
$AM=EM$
$MB=MC$
$\Rightarrow \triangle AMB=\triangle EMC$ (c.g.c)
b.
Vì $\triangle AMB=\triangle EMC$ nên $\widehat{MAB}=\widehat{MEC}$
Mà 2 góc này ở vị trí so le trong nên $EC\parallel AB$
Mà $AB\perp AC$ nên $EC\perp AC$ (đpcm)
c.
Vì $\triangle AMB=\triangle EMC$ nên:
$AB=EC$
Vì $EC\perp AC$ nên $\widehat{ECA}=90^0=\widehat{BAC}$
Xét tam giác $ECA$ và $BAC$ có:
$\widehat{ECA}=\widehat{BAC}=90^0$ (cmt)
$AC$ chung
$EC=BA$ (cmt)
$\Rightarrow \triangle ECA=\triangle BAC$ (c.g.c)
$\Rightarrow EA=BC$
Mà $EA=2AM$ nên $2AM=BC$ (đpcm)

Câu hỏi của le thu giang - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo bài làm tương tự ở link trên.

a) Xét t/giác AMB và t/giác EMC
có MA = ME (gt)
BM = MC (gt)
\(\widehat{AMB}=\widehat{EMC}\)(đối đỉnh)
=> t/giác AMB = t/giác EMC (c.g.c)
b) Do t/giác AMB = t/giác EMC (cmt)
=> \(\widehat{BAM}=\widehat{MEC}\)(2 góc t/ứng)
mà 2 góc này ở vị trí so le trong
=> AB // CE
=> \(\widehat{A}+\widehat{C}=180^0\) (trong cùng phía)
mà \(\widehat{A}=90^0\) => \(\widehat{C}=90^0\) => AC \(\perp\)CE
c) Xét t/giác ABC vuông tại A có AM là đường trung tuyến
=> AM = BM = MC = 1/2BC
=> BC = 2AM
HD C2: CM t/giác ABC = t/giác CEA (C.g.c)
=> BC = EA (2 cạnh t/ứng
=> 1/2BC = 1/2EM
=> 1/2BC = MA (vì EM = MA = 1/2EM)
=> AM = 2BC

Câu hỏi của le thu giang - Toán lớp 7 - Học toán với OnlineMath