Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

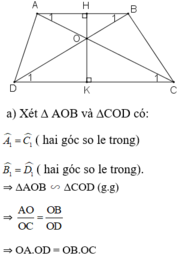
a: Xét ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOB=góc COD
=>ΔOAB đồng dạng vơi ΔOCD
=>OA/OC=OB/OD=AB/CD
=>OA*OD=OB*OC
b: OA/OC=AB/CD
=>OA/6=5/10=1/2
=>OA=3cm
Xet ΔADC có OE//DC
nên OE/DC=AO/AC
=>OE/10=3/(3+6)=3/9=1/3
=>OE=10/3cm

a: Xét ΔAOB và ΔCOD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{COD}\)
Do đó: ΔAOB\(\sim\)ΔCOD
Suy ra: OA/OC=OB/OD
hay \(OA\cdot OD=OB\cdot OC\)
b: Xét ΔADC có MO//DC
nên MO/DC=AM/AD(1)
Xét ΔBDC có ON//DC
nên ON/DC=BN/BC(2)
Xét hình thang ABCD có MN//AB//CD
nên AM/AD=BN/BC(3)
Từ (1), (2) và (3) suy ra OM=ON
hay O là trung điểm của MN

MN//AB => NO//AB; MO//AB; NO//DC( cùng song song với AB)
Áp dụng hệ quả đl Talet vào:
+) tgABC có NO//AB => \(\frac{NO}{AB}=\frac{CN}{CB}\) (1)
+) tgABD có MO//AB => \(\frac{MO}{AB}=\frac{DO}{DB}\) (2)
+) tgBDC có NO//DC => \(\frac{DO}{DB}=\frac{CN}{CB}\) (3) Từ (1),(2),(3) => \(\frac{NO}{AB}=\frac{MO}{AB}\) => NO=MO. Mà: O nằm trên MN => O là trung điểm của MN => ĐPCM
a) Xét hình thang ABCD có AB//CD => \(\widehat{A_1}=\widehat{C_1}\)và \(\widehat{B_1}=\widehat{D_1}\)
\(\Rightarrow\Delta AOB~\Delta COD\left(g.g\right)\)
=> \(\frac{OA}{OC}=\frac{OB}{OD}\Rightarrow OA\cdot OD=OB\cdot OC\)
b) Chứng minh \(\Delta AHO~\Delta CKO\left(g.g\right)\)
\(\frac{OH}{OK}=\frac{AH}{CK}\left(1\right)\)tương tự ta có:
\(\Delta BHO~\Delta DKO\left(g.g\right)\Rightarrow\frac{OH}{OK}=\frac{BH}{DK}\left(2\right)\)
Từ (1) (2) => \(\frac{OH}{OK}=\frac{AH}{CK}=\frac{BH}{DK}=\frac{AH+BH}{CK+DK}=\frac{AB}{CD}\)
vậy \(\frac{OH}{OK}=\frac{AB}{CD}\Rightarrow OH\cdot CD=OK\cdot AB\)

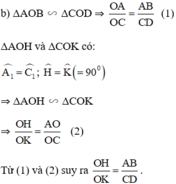
MN//CD⇒OB/BD=NO/CD, AO/AC=OM/CD
mà OA/AC=OB/BD⇒MO=NO
=> O là trung điểm của MN Đây nek~~~