Bài 1. Cho đoạn thẳng AB, M là điểm nằm trên đoạn thẳng AB sao cho \(\frac{MA}{MB}=\frac{7}{4}\). Tính các tỉ số \(\frac{MA}{MB}và\frac{AB}{MB}\)

Bài 2. Cho đoạn thẳng AB=10cm, M là 1 điểm nằm trong đoạn thẳng AB sao cho \(\frac{MA}{MB}=\frac{2}{3}.\) Tính độ dài MA và MB.

Bài 3. Cho AB=6cm. Một điểm C ở trong đoạn AB mà CA=3,6cm. Trên đường thẳng AB về phía B. Hãy tìm một điểm D sao cho: \(\frac{DA}{DB}=\frac{CA}{CB}\)

bài 1: Gọi M là điểm nằm trên đoạn thẳng AB sao cho \(\frac{AM}{AB}=\frac{1}{2}\)

Tính các tỉ số \(\frac{AM}{AB}\)và \(\frac{MB}{AB}\)

bài 2:cho điểm C thuộc đpạn thẳng AB 

a)biết AB=20cm \(\frac{CA}{CB}=\frac{2}{3}\)tính độ dài CA CB

b)biết \(\frac{AC}{AB}=\frac{m}{n}\)tính tỉ số \(\frac{AC}{CB}\)

bài 3:cho đoạn thẳng AB ,điểm C thuộc đoạn thẳng AB ,điểm D thuộc tia đối của tia BA sao cho \(\frac{CA}{CD}=\frac{DA}{DB}=2\)biết CD=4cm

tính độ dài AB

Mỗi câu sau đây đúng hay sai?

a) Nếu điểm M nằm giữa hai điểm A, B thì nó là trung điểm của đoạn thẳng AB.

b) Nếu MA = MB thì M là trung điểm của đoạn thẳng AB.

c) Nếu MA + MB = AB thì M là trung điểm của đoạn thẳng AB.

d) Nếu AM = AB/2 thì M là trung điểm của đoạn thẳng AB.

e) Nếu MA + MB = AB và MA = MB thì M là trung điểm của đoạn thẳng AB.

f) Nếu MA = MB = AB/2 thì M là trung điểm của đoạn thẳng AB.

g) Nếu ba điểm A, M, B thẳng hàng, điểm M nằm giữa hai điểm A, B và AM = AB/2 thì M là trung điểm của đoạn thẳng AB.

Bài 4. Cho ba đoạn thẳng AB, CD, EF sao cho \(\frac{AB}{CD}=\frac{2}{3}\) và \(\frac{CD}{EF}=\frac{4}{6}\). Hãy tính độ dài AB, CD, EF biết rằng: AB+CD+EF=70cm

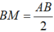
Bài 5. Cho bốn điểm A, N, B, M theo thứ tự cùng nằm trên một đường thẳng sao cho \(\frac{MA}{MB}=\frac{NA}{NB}=\frac{3}{2}\). Tính NA; NB; MA;MB biết rằng AB=6cm

Đề 4 : 

Bài 1 : Cho 3 số : 1 400 , 1 250 , 1 120

a. Phân tích các số trên ra thừa số nguyên tố 

b. Tìm ƯCLN ( 1 400 , 1 250 ) và BCNN ( 1 250 , 1 120)

Bài 2 :Trên tia Ox , lấy 2 điểm A , B sao cho OA = 4cm , OB = 8cm 

a. Tính độ dài đoạn thẳng AB = ?

b. Điểm A có là trung điểm của đoạn thẳng OB không ? Vì sao ?

c. Trên tia đối của tia Ox , lấy điểm C sao cho OC = 6cm 

   Gọi M  là trung điểm của OC .Tính độ dài đoạn thẳng MB =?

Bài 1:Cho đoạn thẳng AB = 4cm gọi O là trung điểm của đoạn thẳng AB , trên tia OA lấy điểm E , trên tia OB lấy điểm F sao cho OE = OF = 3cm , chứng tỏ AE = BF.

Bài 2:Trên tia Ox vẽ 2 điểm A và B sao cho OA = 2cm ; OB = 5cm , gọi M là trung điểm của đoạn thẳng AB:

a) Tính đoạn thẳng AB ; AM

b) Chứng tỏ A nằm giữa O và M.

Giúp mình nhé ! Thank you !!!