mn giúp em vs em đang gấp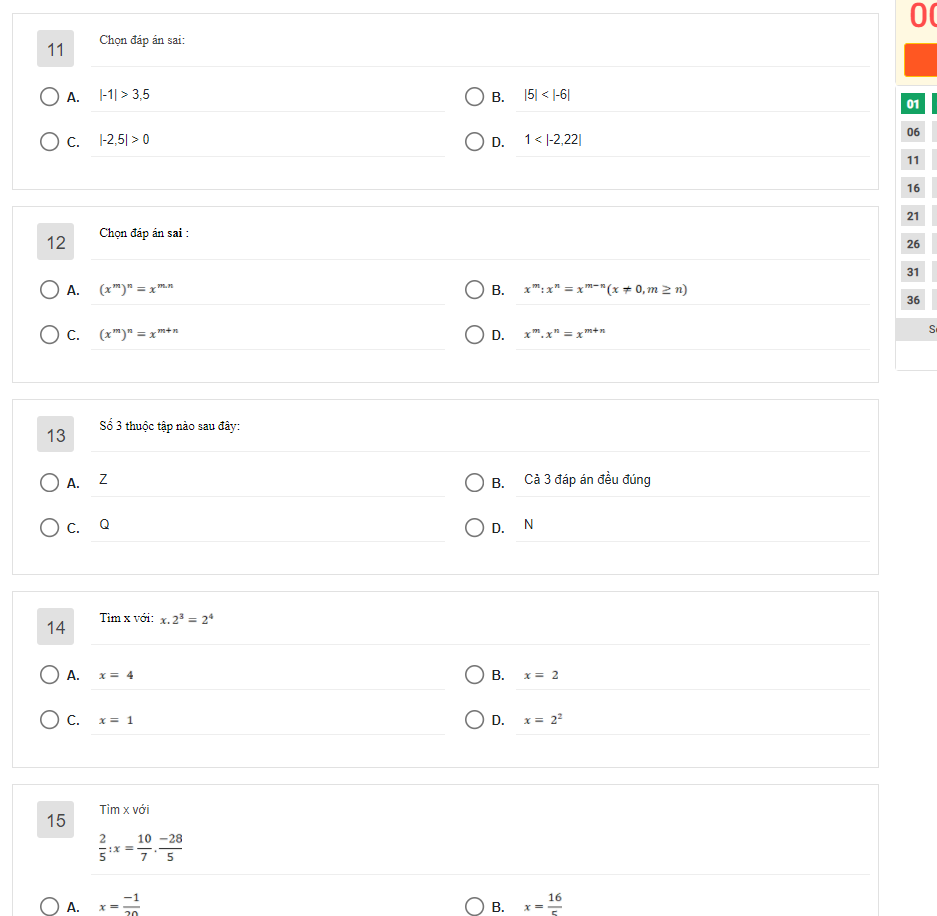

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


e) \(20\%\cdot1\dfrac{1}{4}\cdot12\cdot\dfrac{25}{45}\cdot0,6\)
\(=\dfrac{1}{5}\cdot\dfrac{5}{4}\cdot\dfrac{12}{1}\cdot\dfrac{5}{9}\cdot\dfrac{6}{10}\)
\(=1\)

Tham khảo
Trong bài “Đường đến ngày vinh quang” của cố nhạc sĩ, ca sĩ Trần Lập đã có những lời ca thật ý nghĩa “ Chặng đường nào trải bước trên hoa hồng. Bàn chân cũng thấm đau vì những mũi gai, Đường vinh quang đi qua muôn ngàn sóng gió”. “Chặng đường” ở đây không phải hình ảnh tả thực mà nó là ẩn dụ cho con đường đời, là đích đến của những mục tiêu, nơi con người sẽ chinh phục con đường đó. “Mũi gai” là những khó khăn, thử thách mà con người sẽ phải trải qua nếu như muốn hoàn thiện hành trình đến đích thành công của mình. “Đường vinh quang” là con đường vẻ vang, ý nghĩa nhất mà sau khi vượt qua trăm ngàn sóng gió. “Chặng đường nào trải bước trên hoa hồng. Bàn chân cũng thấm đau vì những mũi gai. Đường vinh quang đi qua muôn ngàn sóng gió”, là những lời ca đầy ý nghĩa về những cố gắng, những nỗ lực của con người trên hành trình chinh phục những đỉnh cao. Có lẽ cũng bởi những ý nghĩa, triết lí vô sâu sắc ấy mà bài hát Đường đến đỉnh vinh quang của cố nhạc sĩ Trần Lập đã vực dậy tinh thần cho hàng ngàn trái tim khán giả trước khi đứng trước khó khăn của cuộc đời. Trên mỗi chặng đường, để đi được đến đích, như một lẽ tất yếu của tự nhiên, con người phải trải qua muôn vàn những khó khăn “bàn chân cũng thấm đau vì những mũi gai”. Đó là những thử thách cực độ, là những khó khăn tưởng chừng có thể làm chúng ta gục ngã, không thể vượt qua. Nhưng nếu có nghị lực, ý chí và niềm tin con người sẽ có thể vượt qua tất cả, những cố gắng ấy sẽ rút ngắn con đường đi đến vinh quang, mang đến những bài học ý nghĩa, nhờ vậy mà chúng ta trưởng thành, mạnh mẽ và bản lĩnh hơn trong cuộc sống. Đỉnh vinh quang là phần thưởng xứng đáng cho những ai biết nỗ lực, cố gắng. Nó không dành cho những người thiếu nỗ lực, những kẻ bỏ cuộc, cái giá của vinh quang rất đắt vì phải trải qua “muôn ngàn sóng gió” nhưng ý nghĩa mà nó mang lại cũng thật to lớn, vẻ vang.



a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.


Tham khảo:
Tầm quan trọng của việc ăn uống đối với sức khỏe của con người:
- Để nuôi sống con người. Nếu không hấp thụ dinh dưỡng từ thức ăn, nước uống con người sẽ chết.
- Để phát triển. Nếu một đứa trẻ không hấp thụ đủ dinh dưỡng cần thiết từ việc ăn uống sẽ dẫn đến thiếu nhiều chất cần thiết cho cơ thể. Hạn chế về phát triển về thể chất cũng như tinh thần, gây một số loại bệnh, hệ miễn dịch kém…

1) \(\sqrt{2x-5}=7\)
\(\left(\sqrt{2x-5}\right)^2=7^2\)
\(2x-5=49\)
\(2x=54\)
\(x=27\)
2) \(3+\sqrt{x-2}=4\)
\(\sqrt{x-2}=1\)
\(\left(\sqrt{x-2}\right)^2=1^2\)
\(x-2=1\)
\(x=3\)
1) \(\sqrt{2x-5}=7\left(đk:x\ge\dfrac{5}{2}\right)\)
\(\Leftrightarrow2x-5=49\Leftrightarrow2x=54\Leftrightarrow x=27\left(tm\right)\)
2) \(3+\sqrt{x-2}=4\left(đk:x\ge2\right)\)
\(\Leftrightarrow\sqrt{x-2}=1\Leftrightarrow x-2=1\Leftrightarrow x=3\)
3) \(\Leftrightarrow\sqrt{\left(x-1\right)^2}=1\Leftrightarrow\left|x-1\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=1\\x-1=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
4) \(\Leftrightarrow\sqrt{\left(x-2\right)^2}=1\Leftrightarrow\left|x-2\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
5) \(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=\sqrt{\left(x+4\right)^2}\)
\(\Leftrightarrow\left|2x-1\right|=\left|x+4\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x+4\\2x-1=-x-4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
6) \(ĐK:x\ge-2\)
\(\Leftrightarrow5\sqrt{x+2}-3\sqrt{x+2}-\sqrt{x+2}=\sqrt{x+7}\)
\(\Leftrightarrow\sqrt{x+2}=\sqrt{x+7}\)
\(\Leftrightarrow x+2=x+7\Leftrightarrow2=7\left(VLý\right)\)
Vậy \(S=\varnothing\)
7) \(ĐK:x\ge-1\)
\(\Leftrightarrow5\sqrt{2x+1}+3\sqrt{x+1}=4\sqrt{x+1}+4\sqrt{2x+1}\)
\(\Leftrightarrow\sqrt{2x+1}=\sqrt{x+1}\)
\(\Leftrightarrow2x+1=x+1\Leftrightarrow x=0\left(tm\right)\)


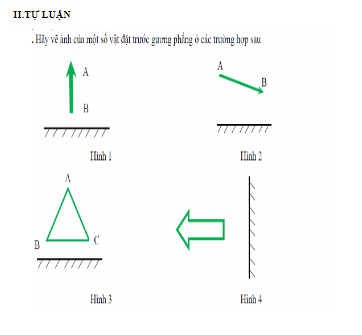
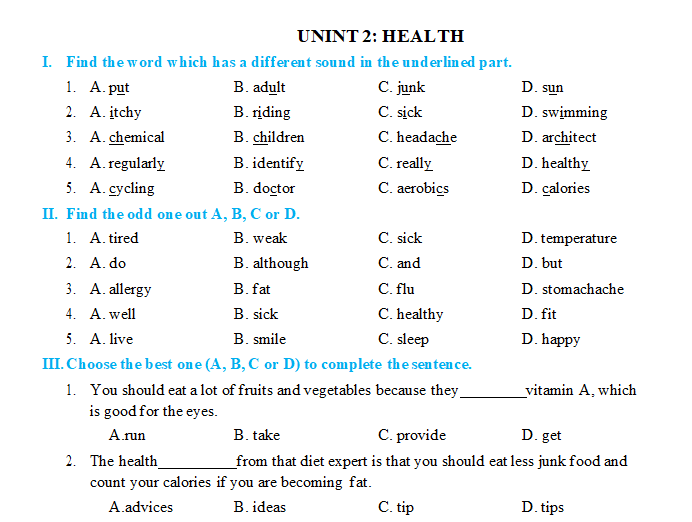






\(11,A\\ 12,C\\ 13,B\\ 14,B\\ 15,A\)