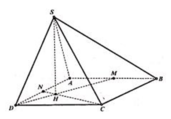
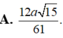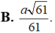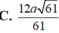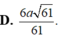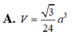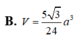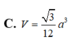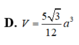Cho hình chóp S.ABCDS.ABCD có đáy ABCDABCD là hình vuông cạnh aa. Gọi MM và NN lần lượt là trung điểm các cạnh ABAB và ADAD; HH là giao điểm của CNCN và DMDM. Biết SHSH vuông góc với mặt phẳng (ABCD)(ABCD) và SH=2\sqrt{2}aSH=22a. Thể tích khối chóp S.CDMNS.CDMN bằng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 6 2019
Đáp án B
Ta có: S B A ^ = 60 ∘ ⇒ S A = A B tan 60 ∘ = a 3
V A . A C D = 1 3 S A . S A C D = 1 3 . a 3 . a 2 2 = a 3 3 6
Lại có: V S . A M N V S . A C D = S M S C . S N S D = 1 4 ⇒ V S . A M N = a 3 3 24
CM
30 tháng 1 2019
Xét các hình vuông ABCD. Ta có hai tam giác vuông ADM và DCN bằng nhau nên ∠ DMA = ∠ CND. Từ đó suy ra DM ⊥ CN. Trong tam giác vuông CDN ta có:
CD 2 = CH.CN ⇒ CH = 2a/ 5
Suy ra SH = CH.tan60
°
= 
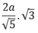
S CDNM = S ABCD - S AMN - S BCM = 5 a 2 / 8
V
S
.
CDNM
= 
CM
1 tháng 6 2017
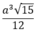
Đáp án C
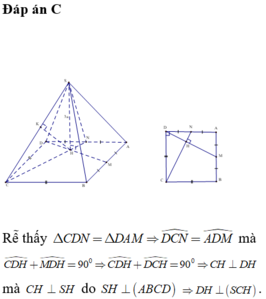
Rễ thấy Δ C D N = Δ D A M ⇒ D C N ^ = A D M ^
mà C D H ^ + M D H ^ = 90 0 ⇒ C D H ^ + D C H ^ = 90 0 ⇒ C H ⊥ D H
mà C H ⊥ S H do S H ⊥ A B C D ⇒ D H ⊥ S C H .
Như vậy kẻ H K ⊥ S C thì HK là đường vuông góc chung của DM và SC hay HK là khoảng cách cần xác định.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
C D 2 = C H . C N ⇒ C H = C D 2 C N = C D 2 C D 2 + D N 2 = 4 a 2 4 a 2 + a 2 = 2 a 5
1 H K 2 = 1 S H 2 + 1 C H 2 = 1 9 a 2 + 5 16 s 2 = 61 144 a 2 ⇒ H K = 12 a 61 61
CM
28 tháng 11 2019
Vì S H ⊥ A B C D nên
V S . C D M N = 1 3 S H . S . C D M N = 1 3 S H . S A B C D - S B C M - S A M N = 1 3 a 3 5 8 a 2 = 5 3 24 a 3
Đáp án B
CM
8 tháng 10 2017
Chọn A.
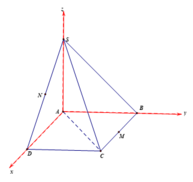
Gắn hệ trục tọa độ như hình vẽ. Khi đó ta có:
A(0;0;0), B(0;a;0), C(a;a;0), D(a;0;0), S(0;0;a)
M là trung điểm của BC ⇒ M a 2 ; a ; 0
N là trung điểm của SD ⇒ N a 2 ; 0 ; a 2 ⇒ M N → 0 ; - a ; a 2
Do ABCD là hình vuông nên AC ⊥ BD
S A ⊥ ( A B C D ) B D ⊂ ( A B C D ) ⇒ S A ⊥ B D
Ta có:
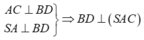
là một pháp tuyến của (SAC)
Khi đó ta có:
sin α = cos ( M N → , B D → ) = M N → . B D → M N → . B D →
= a 2 a 5 2 . a 2 = 10 5
1 sin 2 α = 1 + c o t 2 α ⇔ 25 10 = 1 + c o t 2 α ⇔ c o t 2 α = 3 2 ⇒ c o t α = 3 2 ( d o 0 < α < 90 0 )
Lại có:
tan α . c o t α = 1 ⇒ tan α = 2 3 = 6 3
CM
23 tháng 3 2019
Chọn A.
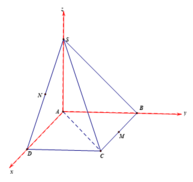
Gắn hệ trục tọa độ như hình vẽ. Khi đó ta có:
A(0;0;0), B(0;a;0), C(a;a;0), D(a;0;0), S(0;0;a)
M là trung điểm của BC ⇒ M a 2 ; a ; 0
N là trung điểm của SD ⇒ N a 2 ; 0 ; a 2 ⇒ M N → 0 ; - a ; a 2
Do ABCD là hình vuông nên AC ⊥ BD
S A ⊥ ( A B C D ) B D ⊂ ( A B C D ) ⇒ S A ⊥ B D
Ta có:
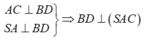
là một pháp tuyến của (SAC)
Khi đó ta có:
sin α = cos ( M N → , B D → ) = M N → . B D → M N → . B D →
= a 2 a 5 2 . a 2 = 10 5
1 sin 2 α = 1 + c o t 2 α ⇔ 25 10 = 1 + c o t 2 α ⇔ c o t 2 α = 3 2 ⇒ c o t α = 3 2 ( d o 0 < α < 90 0 )
Lại có:
tan α . c o t α = 1 ⇒ tan α = 2 3 = 6 3