tìm các giá trị thực của m để
y=x3−(m+1)x2−(2m2−3m+2)x+m(2m−1) đồng biến trên...
Đọc tiếp
tìm các giá trị thực của m để
y=x3−(m+1)x2−(2m2−3m+2)x+m(2m−1) đồng biến trên [2;+∞]
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 9 2017
Đáp án C
Ta có: y’ = 3x2 + 2(m+1)x – (3m+2)
Hàm số đồng biến trên khoảng (0;1)
3x2 + 2(m+1)x – (3m+2) ≥ 0 ∀ x ∈ (0;1)
⇔ m ≤ − 3 x 2 + 2 x − 2 2 x − 3 ∀ x ∈ (0;1)
Xét hàm số: g = − 3 x 2 + 2 x − 2 2 x − 3 D =(0;1)
Ta có: g’ = − 6 x 2 − 18 x − 2 ( 2 x − 3 ) 2
ð g’ = 0 ⇔ x = 9 ± 93 6 (không thoản mãn)
Ta có bảng biến thiên
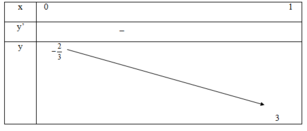
Vậy với m ≤ 3 hàm số đồng biến trên khoảng (0;1)
tại sao \(\frac{x1+x2}{2}< 2\) ạ
\(y'=g\left(x\right)=3x^2-2\left(m+1\right)x-\left(2m^2-3m+2\right)\)
Để hàm số đồng biến trên khoảng đã cho
\(\Leftrightarrow g\left(x\right)\ge0;\forall x\ge2\)
\(\Delta'=\left(m+1\right)^2+3\left(2m^2-3m+2\right)=7\left(m-\frac{1}{2}\right)^2+\frac{21}{4}>0;\forall m\)
\(\Rightarrow\) Để \(g\left(x\right)\ge0;\forall x\ge2\Leftrightarrow x_1< x_2\le2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1-2\right)\left(x_2-2\right)\ge0\\\frac{x_1+x_2}{2}< 2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2-2\left(x_1+x_2\right)+4\ge0\\x_1+x_2< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\frac{1}{3}\left(2m^2-3m+2\right)-\frac{4}{3}\left(m+1\right)+4\ge0\\\frac{2}{3}\left(m+1\right)< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2m^2-m+6\ge0\\2m< 10\end{matrix}\right.\) \(\Rightarrow-2\le m\le\frac{3}{2}\)