Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a.ta có: \(3^{2009}\)
\(9^{1005}\)= \(\left(3^2\right)^{1005}\) =\(3^{2010}\)
*Vì 2010> 2009 =>\(3^{2009}\) < \(3^{2010}\)
Vậy \(3^{2009}\) < \(9^{1005}\).
n^150<5^225
(n^2)^75<(5^3)^75
n^2<5^3
n^2<125
mà n lớn nhất nên n^2=121
n=11
chính xác 100%
n150<5225
=>(n2)75<(53)75
=>n2<53=125
=>n<12
=>max n=11
vậy max n=11 max là giá trị lớn nhất
Ta có: n^150 < 5^225
<=> n^2^75< 5^3^75
<=> n^2 < 5^3= 125
<=> n^2 ≤ 121
<=>n ≤11
mà n lớn nhất nên n=11
Vậy n=11
1 , (3/7)^21 :(9/49)^6
= (3/7)^21 : [(3/7)^2]^6
= (3/7)^21 : (3/7)12
= (3/7)^9
2, a) 291 và 535
ta có: 291 < 290 = (25)18 = 3218
lại có: 3218 > 2518 = (52)18 = 536 > 535
vậy 291 > 535
b) 34000 và 92000
ta có: 34000 = (34)1000 = 811000
92000 = (92)1000 = 811000
vậy 34000 = 92000
c) 2332 và 3223
ta có: 2332 < 2333 = (23)111 = 8111
3223 > 3222 = (32)111 = 9111
mà 8111 < 9111
vậy 2332 < 3223
3. n150 = (n2 )75 < 5225 = (53)75 => n2 < 53 = 125 => n2 lớn nhất = 121 => n =11.
4. M=22010-(22009+22008+22007+...+21+20)
M=22010-22009-22008-22007-...-21-20
=>2M=22011-22010-22009-22008-...-22-21
=>2M-M=22011-22010-22009-22008-...-22-21-(22010-22009-22008-22007-...-21-20)
=>M=22011-22010-22009-22008-...-22-21-22010+22009+22008+22007+...+21+20
=22011-22010-22010+20
=22011-2.22010+1
=22011-22011+1
=1
Vậy M=1
\(Bai1:\left(\frac{3}{7}\right)^{21}:\left(\frac{9}{49}\right)^6=\frac{3^{21}}{7^{21}}:\frac{\left(3^2\right)^6}{\left(7^2\right)^6}=\frac{3^{21}}{7^{21}}:\frac{3^{12}}{7^{12}}=\frac{3^{21}}{7^{21}}.\frac{7^{12}}{3^{12}}=\frac{3^9}{7^9}\)
Bài 2: a) 291 = (213)7 = 81927
535 = (55)7 = 31257
Vì 81927 > 31257
=> 291 > 535
b) 34000 = (32)2000 = 92000
=> 34000 = 92000
c) 2332 < 2333 = (23)111 = 8111
3223 > 3222 = (32)111 = 9111
Vì 8111 < 9111
=> 2332 < 3223
Bài 3: n150 < 5225
=> (n2)75 < (53)75
=> n2 < 53
=> n2 < 125
Mà n lớn nhất => n2 lớn nhất => n2 = 121
=> n = 11
Bài 4: Đặt A = 22009 + 22008 + ... + 21 + 20
A = 20 + 21 + ... + 22008 + 22009
2A = 21 + 22 + ... + 22009 + 22010
2A - A = (21 + 22 + ... + 22009 + 22010) - (20 + 21 + ... + 22008 + 22009)
A = 22010 - 20
A = 22010 - 1
=> M = 22010 - (22010 - 1)
M = 22010 - 22010 + 1
M = 1
Bài 1:
a. $2^{29}< 5^{29}< 5^{39}$
$\Rightarrow A< B$
b.
$B=(3^1+3^2)+(3^3+3^4)+(3^5+3^6)+...+(3^{2009}+3^{2010})$
$=3(1+3)+3^3(1+3)+3^5(1+3)+...+3^{2009}(1+3)$
$=(1+3)(3+3^3+3^5+...+3^{2009})$
$=4(3+3^3+3^5+...+3^{2009})\vdots 4$
Mặt khác:
$B=(3+3^2+3^3)+(3^4+3^5+3^6)+....+(3^{2008}+3^{2009}+3^{2010})$
$=3(1+3+3^2)+3^4(1+3+3^2)+...+3^{2008}(1+3+3^2)$
$=(1+3+3^2)(3+3^4+....+3^{2008})=13(3+3^4+...+3^{2008})\vdots 13$
Bài 1:
c.
$A=1-3+3^2-3^3+3^4-...+3^{98}-3^{99}+3^{100}$
$3A=3-3^2+3^3-3^4+3^5-...+3^{99}-3^{100}+3^{101}$
$\Rightarrow A+3A=3^{101}+1$
$\Rightarrow 4A=3^{101}+1$
$\Rightarrow A=\frac{3^{101}+1}{4}$
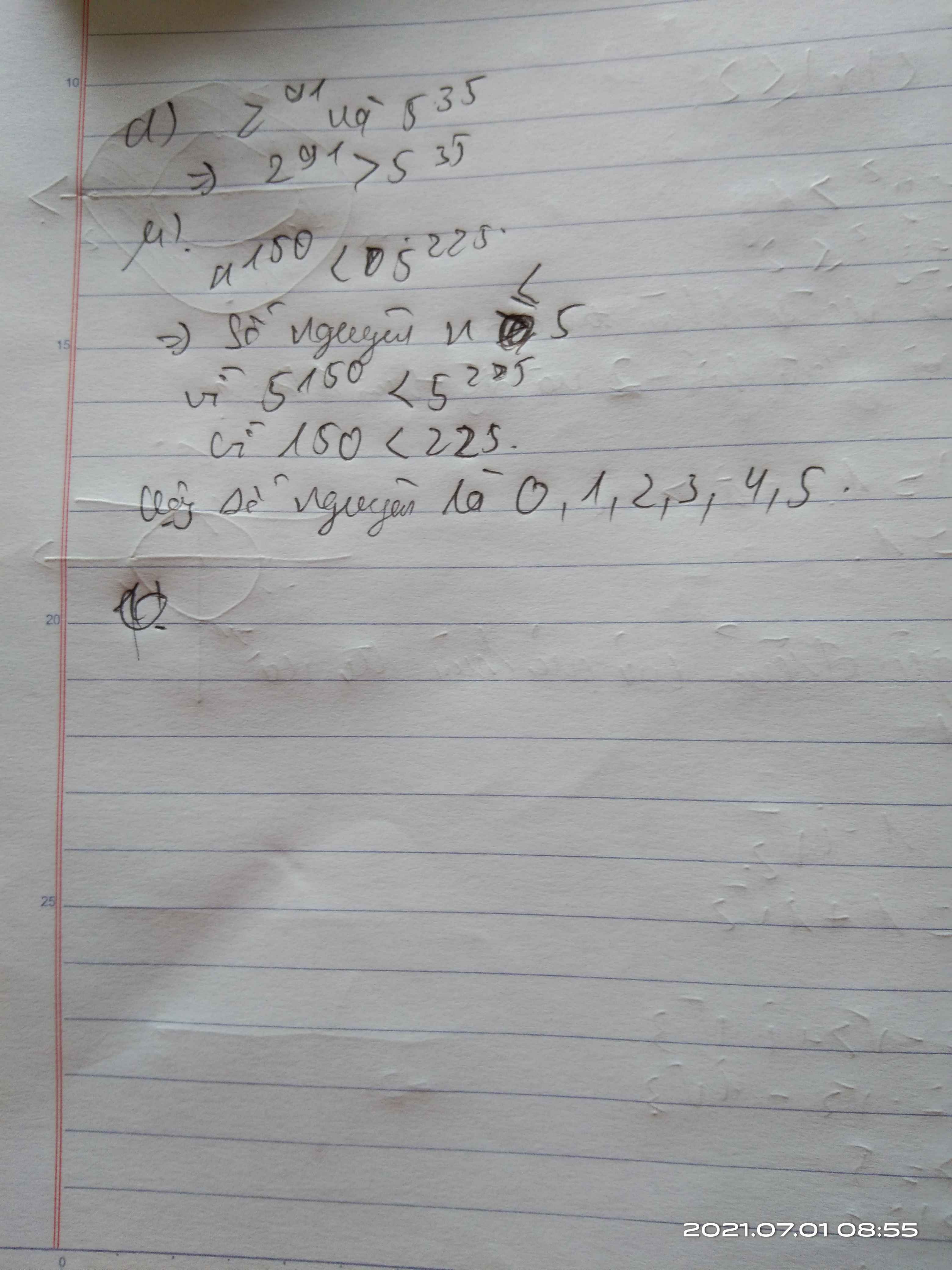
bài 4 : c1 \(3^{4000}\)và \(9^{2000}\)
\(\Leftrightarrow9^{2000}\Leftrightarrow\left(3^2\right)^2^{000}\Leftrightarrow3^{4000}\)
vì \(3^{4000}=3^{4000}\Leftrightarrow3^{4000}=9^{2000}\)
c2
ta có
\(3^{4000}=\left(3^4\right)^{1000}=81^{1000}\)
\(9^{2000}=\left(9^2\right)^{1000}=81^{1000}\)
vì \(81^{1000}=81^{1000}\Leftrightarrow3^{4000}=9^{2000}\)
bài 5
\(2^{332}< 2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{223}>3^{222}=\left(3^2\right)^{111}=9^{111}\)
vì \(8^{111}< 9^{111}\Leftrightarrow2^{332}< 3^{223}\)
3) M = 22010 - (22009 + 22008 + .... + 21 + 20)
Đặt N = 22009 + 22008 + .... + 21 + 20
=> 2N = 22010 + 22009 + .... + 22 + 21
=> 2N - N = (22010 + 22009 + .... + 22 + 21) - (22009 + 22008 + .... + 21 + 20)
=> N = 22010 - 1
Khi đó M = 22010 - (22010 - 1) = 1
4) C1 Ta có 34000 = (34)1000 = 811000 = (92)1000 = 92000
34000 = 92000
C2 Ta có : 34000 = (34)1000 = 811000 (1)
Lại có 92000 = (92)1000 = 811000 (2)
Từ (1) (2) => 34000 = 92000
5 Ta có 2332 < 2333 = (23)111 = 8111 < 9111 = (32)111 = 3222 < 3223
=> 2332 < 3223
2) Ta có n150 < 5225
=> (n5)75 < (53)75
=> n5 < 53
=> n5 < 125
Vì n là số nguyên lớn nhất => n = 2