Tìm số tự nhiên n sao cho : \(A=n^3-2n^2+2n-4\) là số nguyên tố
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=n^3-2n^2+2n-4\)
\(=n^2\left(n-2\right)+2\left(n-2\right)\)
\(=\left(n-2\right)\left(n^2+2\right)\)
Để A là số nguyên tố thì \(n-2=1\left(h\right)n^2+2=1\)
Mà \(n^2\ge0\Rightarrow n^2+2\ge2>1\Rightarrow n-2=1\Rightarrow n=3\)
Thay vào A ta được A=11 ( LSNT )
Vậy n=3

Bài 1:
Ta có dãy số 2, 4, 6, ..., 2n là một dãy số chẵn liên tiếp.
Ta có công thức tổng của dãy số chẵn liên tiếp là: S = (a1 + an) * n / 2
Với a1 là số đầu tiên của dãy, an là số cuối cùng của dãy, n là số phần tử của dãy.
Áp dụng công thức trên vào bài toán, ta có:
(2 + 2n) * n / 2 = 756
(2n + 2) * n = 1512
2n^2 + 2n = 1512
2n^2 + 2n - 1512 = 0
Giải phương trình trên, ta được n = 18 hoặc n = -19.
Vì n là số tự nhiên nên n = 18.
Vậy số tự nhiên n cần tìm là 18.
Bài 2:
Ta có p = (n - 2)(n^2 + n - 5)
Để p là số nguyên tố, ta có hai trường hợp:
1. n - 2 = 1 và n^2 + n - 5 = p
2. n - 2 = p và n^2 + n - 5 = 1
Xét trường hợp 1:
n - 2 = 1
=> n = 3
Thay n = 3 vào phương trình n^2 + n - 5 = p, ta có:
3^2 + 3 - 5 = p
9 + 3 - 5 = p
7 = p
Vậy n = 3 và p = 7 là một cặp số nguyên tố thỏa mãn.
Xét trường hợp 2:
n - 2 = p
=> n = p + 2
Thay n = p + 2 vào phương trình n^2 + n - 5 = 1, ta có:
(p + 2)^2 + (p + 2) - 5 = 1
p^2 + 4p + 4 + p + 2 - 5 = 1
p^2 + 5p + 1 = 1
p^2 + 5p = 0
p(p + 5) = 0
p = 0 hoặc p = -5
Vì p là số nguyên tố nên p không thể bằng 0 hoặc âm.
Vậy không có số tự nhiên n thỏa mãn trong trường hợp này.
Vậy số tự nhiên n cần tìm là 3.
Bài 1
...=((2n-2):2+1):2=756
(2(n-1):2+1)=756×2
n-1+1=1512
n=1512

đặt 2n + 34 = a^2
34 = a^2-n^2
34=(a-n)(a+n)
a-n thuộc ước của 34 là { 1; 2; 17; 34} và a-n . Ta có bảng sau ( mik ko bt vẽ)
=> a-n 1 2
a+n 34 17
Mà tổng và hiệu 2 số nguyên cùng tính chẵn lẻ
Vậy ....
Ta cóS = 14 +24 +34 +···+1004 không là số chính phương.
=> S= (1004+14).100:2=50 900 ko là SCP

Vì 7n+13 và 2n+4 nguyên tố cùng nhau nên ta gọi d = UCLN(7n+13,2n+4)
=>7n+13 ⋮ d và 2n+4 ⋮ d
Có 7n+13 ⋮ d => 2(7n+13) ⋮ d => 14n+26 ⋮ d
2n+4 ⋮ d => 7.(2n+14) ⋮ d => 14n+28 ⋮ d
Suy ra (14n+28) – (14n+26) ⋮ d => 2 ⋮ d => d ∈ {1;2}
Nếu d = 1 thì 7n+13 và 2n+4 là nguyên tố cùng nhau
Nếu d = 2 => 7n+13 ⋮ 2 => 7.(n+1)+6 ⋮ 2 vì 6 ⋮ 2 nên 7.(n+1) ⋮ 2 mà UC(7,2) = 1 => n+1 ⋮ 2
Để n+1 ⋮ 2 thì n = 2k+1
Vậy để 7n+13 và 2n+4 là số nguyên tố cùng nhau thì n ≠ 2k+1

Olm sẽ hướng dẫn em giải những dạng toán nâng cao như này bằng phương pháp đánh giá em nhé.
Nếu n = 2 ta có: 2 + 2 = 4 ( loại)
Nếu n = 3 ta có: 2n + 27 = 2.3 + 27 = 33 (loại)
Nếu n > 3 thì vì n là số nguyên tố nên n có dạng:
n = 3k + 1 hoặc n = 3k + 2
Với n = 3k + 1 ta có: n + 2 = 3k + 1 + 2 = 3k + 3 ⋮ 3 (loại)
Với n = 3k + 2 ta có: n + 10 = 3k + 2 + 10 = 3k + 12 =3.(k+4)⋮3 (loại)
Không có số tự nhiên nào thỏa mãn n+2; n+10; 2n+27 đồng thời là số nguyên tố.
Kết luận: n \(\in\) \(\varnothing\)

Gọi ƯC(7n+13,2n+4)=d
Ta có: 7n+13 chia hết cho d=>2.(7n+13) chia hết cho d=>14n+26 chia hết cho d
2n+4 chia hết cho d=>7.(2n+4) chia hết cho d=>14n+28 chia hết cho d
=>14n+28-(14n+26) chia hết cho d
=>2 chia hết cho d
=>d=Ư(2)={1,2}
Để 7n+13 và 2n+4 à số nguyên tố cùng nhau
=>ƯC(7n+13,2n+4)=1
=>d=1
=>d khác 2
=>7n+13 không chia hết cho 2
mà 13 không chia hết cho 2
=>7n chia hết cho 2
Vì (2,7)=1
=>n chia hết cho 2
=>n=2k
Vậy n=2k

Gọi ƯC(4n+3,2n+3)=d
Ta có: 4n+3 chia hết cho d
2n+3 chia hết cho d=>2.(2n+3) chia hết cho d=>4n+6 chia hết cho d
=>4n+6-(4n+3) chia hết cho d
=>4n+6-4n-3 chia hết cho d
=>3 chia hết cho d
=>d=Ư(3)={1,3}
Để 4n+3 và 2n+3 là 2 số nguyên tố cùng nhau
=>ƯC(4n+3,2n+3)=1
=>d=1
=>d khác 3
=>2n+3 không chia hết cho 3
=>2n+3-3 không chia hết cho 3
=>2n không chia hết cho 3
mà (2,3)=1
=>n không chia hết cho 3
=>n khác 3k
Vậy n khác 3k thì (4n+3,2n+3)=1
ta nhân 2n+3 với 2 thì sẽ ra 4n+6.
rồi lấy 4n+6-4n+3=3
Mà ước của 3 gồm 1,3
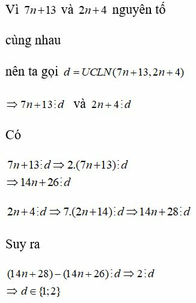

Với n = 0 => A = 03 - 2.02 + 2.0 - 4 = -4 ko là số nguyên tố
n = 1 => A = 13 - 2.12 + 2.1 - 4 = 1 - 2 + 2 - 4 = -3 ko là số nguyên tố
n = 2 => A = 23 - 2.22 + 2.2 - 4 = 0 ko là số nguyên tố
n = 3 => A = 33 - 2.32 + 2.3 - 4 = 11 là số nguyên tố
Với n \(\ge\)4 => A = n3 - 2n2 + 2n - 4 = n2(n - 2) + 2(n - 2) = (n2 + 2)(n - 2) có nhiều hơn 2 ước
=> A là hợp số
Vậy Với n = 3 thì A là số nguyên tố