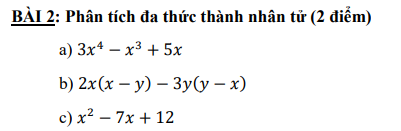1. Những cây sẵn trong tự nhiên, tự bản thân nó được dùng để trang trí: cây hoa (hoa hồng, hoa cẩm chướng..), cây tùng, cây sanh. 
2. Phương pháp sinh sản vô tính: giâm cành bằng cát, ghép, chiết cành, nuôi cấy mô tế bào. 
phương pháp sinh sản hữu tính: thụ phấn trong tự nhiên. 
3. chọn chậu cây cảnh dựa trên các yếu tố: chất liệu, kích thước, 

4. tránh hư hỏng do va đập cơ học

5. Sử dụng axit abxixic để ức chế sinh trưởng. 
6. kỹ thuật sản xuất, an toàn thực phẩm, môi trường làm việc đảm bảo, nguồn gốc sản phẩm rõ ràng. 

E cảm ơn cô nhiều ạ!!

1033/57

\(...=\dfrac{152}{10}-\dfrac{15}{9}+\dfrac{48}{10}-\dfrac{4}{19}=\dfrac{76}{5}-\dfrac{5}{3}+\dfrac{24}{5}-\dfrac{4}{19}\)

\(=\dfrac{76}{5}-\dfrac{5}{3}+\dfrac{24}{5}-\dfrac{4}{19}=\dfrac{76}{5}+\dfrac{24}{5}-\dfrac{5}{3}-\dfrac{4}{19}\)

\(=\dfrac{100}{5}-\dfrac{5}{3}-\dfrac{4}{19}=20-\dfrac{5}{3}-\dfrac{4}{19}=\dfrac{20.57-5.19-4.3}{57}=\dfrac{1033}{57}\)

a: Xét ΔABD và ΔACD có

AB=AC

BD=CD

AD chung

Do đó: ΔABD=ΔACD

b: ΔABD=ΔACD

=>\(\widehat{ADB}=\widehat{ADC}\)

mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)

nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)

c: Ta có: \(\widehat{ADB}=90^0\)

=>AD\(\perp\)BC tại D

D là trung điểm của BC

=>\(DB=DC=\dfrac{BC}{2}=\dfrac{24}{2}=12\left(cm\right)\)

ΔADB vuông tại D

=>\(AD^2+DB^2=AB^2\)

=>\(AD^2=20^2-12^2=256\)

=>\(AD=\sqrt{256}=16\left(cm\right)\)

Xét ΔABC có

AD là đường trung tuyến

G là trọng tâm

Do đó: \(AG=\dfrac{2}{3}AD=\dfrac{2}{3}\cdot16=\dfrac{32}{3}\left(cm\right)\)

2

a) \(=x\left(3x^3-x^2+5\right)\)

b) \(=\left(2x+3y\right)\left(x-y\right)\)

c) \(=\left(x^2-3x\right)-\left(4x-12\right)=x\left(x-3\right)-4\left(x-3\right)=\left(x-3\right)\left(x-4\right)\)

a, = x.(3x³ - x² + 5)

b, = 2x.(x - y) + 3y.(x - y) = (x - y).(2x + 3y)

c, = x² - 3x - 4x + 12 = (x² - 3x) - (4x - 12) = x.(x - 3) - 4.(x - 3) = (x - 3).(x - 4)

dài quá bạn ơi, tách ra làm 3 đến 4 phần đăng riêng nhé

dạ rồi ạ

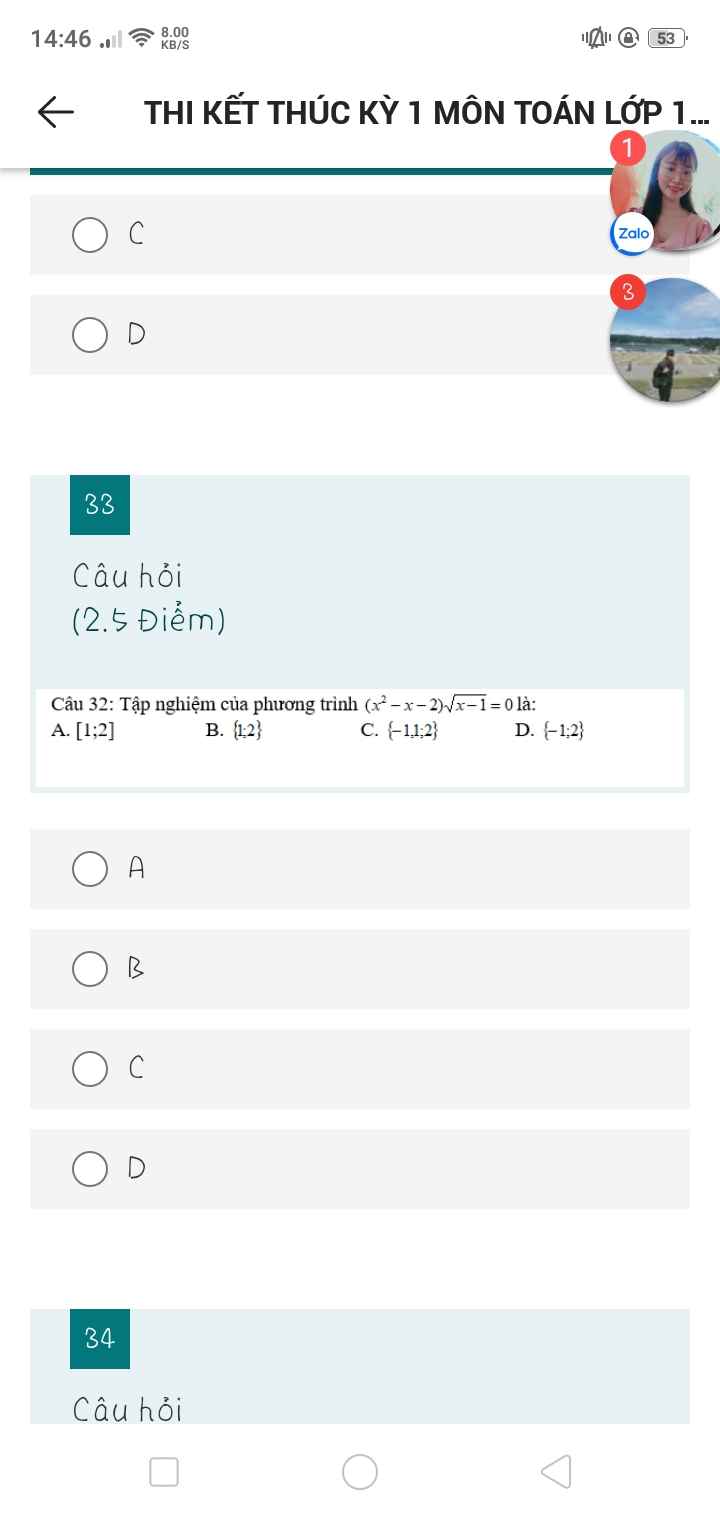
\(\left(x^2-x-2\right)\sqrt{x-1}=0\left(đk:x\ge1\right)\)

\(\Leftrightarrow\left(x-2\right)\left(x+1\right)\sqrt{x-1}=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\end{matrix}\right.\) (do x+1>0)

Ý B.

B

thể tích của vật đó là

`V=m/D =5,2/2600=2*10^(-3) m^3`

Do vật đc nhúng chìm hoàn toàn

nên lực đẩy Ác si mét t/d lên vật là

`F_A= d_n *V=2*10^(-3) *10000=20(N)`

working

directly

best English nha