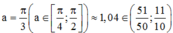Biết diện tích hình phẳng giới hạn bởi các đường y = sinx, y = cosx, x = 0, x = a (với a ∈ π 4 ; π 2 là 1 2 - 3 + 4 2 - 3 . Hỏi số a thuộc khoảng nào sau đây?
A. 11 10 ; 3 2
B. 51 50 ; 11 10
C. 7 10 ; 1
D. 1 ; 51 50
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Đặt f1(x) = cosx, f2(x) =sinx ;
Ta có f1(x) - f2(x) = 0 <=> cosx - sinx = 0 <=> x = 5 π 4 ∈ π 2 ; 3 π 2
Diện tích hình phẳng đã cho là:


Đáp án C
∫ 0 π 2 sin x − cos x d x = − ∫ 0 π 4 sin x − cos x d x + ∫ π 4 π 2 sin x − cos x d x = − 2 ∫ 0 π 4 sin x − π 4 d x + ∫ π 4 π 2 sin x − π 4 d x S = 2 . cos x − π 4 π 4 0 − 2 . cos x − π 4 π 2 π 4 = 2 1 − 1 2 − 2 1 2 − 1 = 2 2 − 2 = 2 2 − 1
“Dùng CASIO tính tích phân trị tuyệt đối, dò đáp án
Đáp án B
Phương pháp: Sử dụng công thức ứng dụng của tích phân để tính diện tích hình phẳng.
Cách giải: Xét phương trình hoành độ giao điểm
sinx = cosx <=> tanx = 1 <=> x = π 4 + k π
TH1: a = π 4 => => không thỏa mãn
=> không thỏa mãn
TH2: a = π 2 =>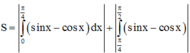
=> không thỏa mãn
TH3: a ∈ π 4 ; π 2
=>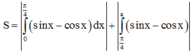
=>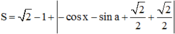
<=>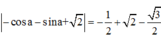
<=>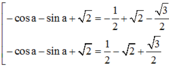
<=>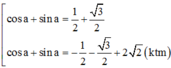
=>