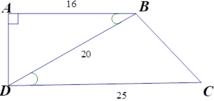
Cho hình thang vuông ABCD (A = D = 90 ∘ ) có AB = 16cm, CD = 25cm, BD = 20cm. Độ dài cạnh BC là
A. 10cm
B. 12cm
C. 15cm
D. 9cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tam giác ABD và BDC có:
B A D ^ = D B C ^ = 60 ∘
A B D ^ = B D C ^ (so le trong)
⇒ Δ A B D đ ồ n g d ạ n g Δ B D C g , g ⇒ A B B D = B D D C ⇒ B D 2 = A B . D C = 4.9 = 36 ⇒ B D = 6 c m
Đáp án: D

ΔABD và ΔBDC có góc ABD = BDC (hai góc ở vị trí so le trong bằng nhau do AB // CD);
Và A B B D = B D D C (vì 16 20 = 20 25 )
Do đó ΔABD ~ ΔBDC (c.g.c)
Đáp án: A

Do góc <DAB = <CBD =90 độ và <ABD = < BDC (do AB//CD)
-> Tam giác ADB và BCD đồng dạng
=> AD/BC = DB/CD <-> AD.CD=BC.DB <-> BC.DB = 12.25 =300 (1)
Mặt khác do tam giác DBC vuông tại B nên theo định lý Pitago :
BD^2+BC^2=CD^2
hay BC^2+BD^2 =625 (2)
Từ (1) và (2) ta giải hệ thì có BC, BD:
BD^2+ (300/BD)^2=625 -> BD^4 - 625 BD^2 +900 = 0 -> BD^2 = (625+can( 387025))/2 ( loại nghiệm còn lại do BD là cạnh huyền của tam giác vuông ABD nên BD^2 > AD^2 =144)
-> BD = can( (625+can( 387025))/2 )
-> BC = 3000/BD
Do góc <DAB = <CBD =90 độ và <ABD = < BDC (do AB//CD)
-> Tam giác ADB và BCD đồng dạng
=> AD/BC = DB/CD <-> AD.CD=BC.DB <-> BC.DB = 12.25 =300 (1)
Mặt khác do tam giác DBC vuông tại B nên theo định lý Pitago :
BD^2+BC^2=CD^2
hay BC^2+BD^2 =625 (2)
Từ (1) và (2) ta giải hệ thì có BC, BD:
BD^2+ (300/BD)^2=625 -> BD^4 - 625 BD^2 +900 = 0 -> BD^2 = (625+can( 387025))/2 ( loại nghiệm còn lại do BD là cạnh huyền của tam giác vuông ABD nên BD^2 > AD^2 =144)
-> BD = can( (625+can( 387025))/2 )
-> BC = 3000/BD
~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~
~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~ Và chúc các bạn trả lời câu hỏi này kiếm được nhiều k hơn ~~~~~~~~~~~~

a) CE = BC – BE = 25 – 9 =16 = CD
Tam giác ABE cân tại B => góc BAE = góc BEA
Tam giác CED cân tại C => góc CED = góc CDE
=> góc BEA + góc CED
= góc BAE + góc CDE
= 90 độ - góc EAD + 90 độ - góc ADE
= 180 độ - (góc EAD + góc ADE)
=180 độ - (180 độ - góc AED)
=góc AED
=> góc BEA + góc CED=góc AED
Mà góc BEA + góc CED + góc AED = 180 độ
=> góc BEA + góc CED=góc AED = 90 độ
Vì ΔABD ~ ΔBDC (cmt) nên góc A = DBC.
Ta có A = 90 ∘ nên DBC = 90 ∘ . Theo định lí Pytago, ta có
B C 2 = C D 2 - B D 2 = 25 2 - 20 2 = 152 . Vậy BC = 15cm
Đáp án: C