Cho hình thang vuông ABCD (A = D = 90 ∘ ) có AB = 16cm, CD = 25cm, BD = 20cm. Tam giác ABD đồng dạng với tam giác nào dưới đây?
A. ΔBDC
B. ΔCBD
C. ΔBCD
D. ΔDCB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 3 2016
1) coi lại đề
2) a) tam giác ABD và tam giác ABC có
góc A=góc A, góc ABD=góc ACB
=> tam giác ABD đồng dạng tam giác ACB (g-g)
b) ta có tam giác ABD đồng dạng tam giác ACB=> AB/AC=AD/AB=> 6/9=AD/6=> AD=(6.6):9=4
24 tháng 8 2022
a: Xét ΔABM vuông tại A và ΔDMC có
BA/DM=AM/CD
nên ΔABM đồng dạng với ΔDMC
b: Ta có: ΔABM đồng dạng với ΔDMC
nên góc AMB=góc DCM
=>góc AMB+góc DMC=góc DCM+góc DMC=90 độ
=>góc BMC=90 độ
=>ΔBMC vuông tại M
c: \(S=MB\cdot\dfrac{MC}{2}=10\cdot\dfrac{20}{2}=100\left(cm^2\right)\)
CM
6 tháng 5 2017
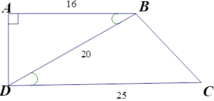
Vì ΔABD ~ ΔBDC (cmt) nên góc A = DBC.
Ta có A = 90 ∘ nên DBC = 90 ∘ . Theo định lí Pytago, ta có
B C 2 = C D 2 - B D 2 = 25 2 - 20 2 = 152 . Vậy BC = 15cm
Đáp án: C
CM
29 tháng 11 2019
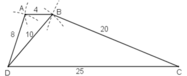
a) Cách vẽ:
- Vẽ ΔBDC:
+ Vẽ DC = 25cm
+ Vẽ cung tròn tâm D có bán kính = 10cm và cung tròn tâm C có bán kính = 20cm. Giao điểm của hai cung tròn là điểm B.
Nối DB và BC.
- Vẽ điểm A: Vẽ cung tròn tâm B có bán kính = 4cm và cung tròn tâm D có bán kính = 8cm. Giao điểm của hai cung tròn này là điểm A.
Nối DA và BA.
Vậy là ta đã vẽ được tứ giác ABCD thỏa mãn điều kiện đề bài.
22 tháng 3 2023
a: Xét ΔOAB vuông tại O và ΔOCD vuông tại O có
góc OAB=góc OCD
=>ΔOAB đồng dạng với ΔOCD
b: Xét ΔABD vuông tại A và ΔDAC vuông tại D có
góc ABD=góc DAC
=>ΔABD đồng dạng với ΔDAC
ΔABD và ΔBDC có góc ABD = BDC (hai góc ở vị trí so le trong bằng nhau do AB // CD);
Và A B B D = B D D C (vì 16 20 = 20 25 )
Do đó ΔABD ~ ΔBDC (c.g.c)
Đáp án: A