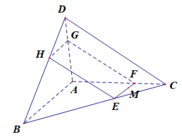
Đáp án C

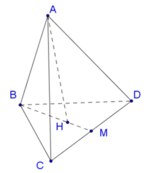
Gọi M là trung điểm của CD, H là trọng tâm của tam giác BCD.

Ta có A H ⊥ B C D  (giả thiết ABCD là tứ diện đều)

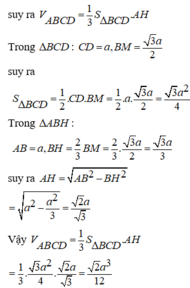
Chọn C

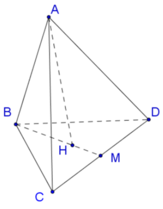
Gọi M là trung điểm của CD, H là trọng tâm của tam giác BCD

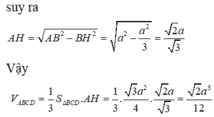
Đáp án B

Gọi M là trung điểm của CD , H là trọng tâm của tam giác BCD.

Ta có AH ⊥ BCD (giả thiết ABCD là tứ diện đều) suy ra

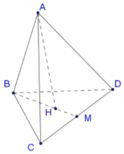
Đáp án A

Ta có d G 1 ; G 2 G 3 G 4 = 1 2 d A ; G 2 G 3 G 4  

= 1 2 . 2 3 d A ; M N P = 1 3 d A ; M N P S G 2 G 3 G 4 = 2 3 2 S M N P = 4 9 . 1 4 S A B C = 1 9 S A B C  

Thể tích của khối tứ diện  G 1 G 2 G 3 G 4  là

V = 1 3 d G 1 ; G 2 G 3 G 4 . S G 2 G 3 G 4 = 1 3 . 1 3 . d A ; M N P . 1 9 S A B C = 1 27 V A B C D = V 27

Đáp án D

Đáp án: A.

§ Hướng dẫn giải:

Dễ dàng ta có được

V A B ' C ' D V A B C D = A B ' A B . A C ' A C = 1 4

Đáp án D

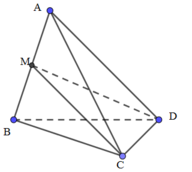
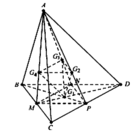
Cách giải:

Mặt phẳng (MCD) chia khối tứ diện ABCD thành hai khối đa diện là: A.MCD và M.BCD