a) \(M(x) = A(x) + B(x) \\= 4{x^4} + 6{x^2} - 7{x^3} - 5x - 6 - 5{x^2} + 7{x^3} + 5x + 4 - 4{x^4} \\=(4x^4-4x^4)+(-7x^3+7x^3)+(6x^2-5x^2)+(-5x+5x)+(-6+4)\\= {x^2} - 2.\)

b) \(A(x) = B(x) + C(x) \Rightarrow C(x) = A(x) - B(x)\)

\(\begin{array}{l}C(x) = A(x) - B(x)\\ = 4{x^4} + 6{x^2} - 7{x^3} - 5x - 6 - ( - 5{x^2} + 7{x^3} + 5x + 4 - 4{x^4})\\ = 4{x^4} + 6{x^2} - 7{x^3} - 5x - 6 + 5{x^2} - 7{x^3} - 5x - 4 + 4{x^4}\\ =(4x^4+4x^4)+(-7x^3-7x^3)+(6x^2+5x^2)+(-5x-5x)+(-6-4)\\= 8{x^4} - 14{x^3} + 11{x^2} - 10x - 10\end{array}\) 

B(3)=2*3^2-4*3+3=18-12+3=9

B(-1/2)=2*1/4-4*(-1/2)+3=1/2+3+2=1/2+5=11/2

Cảm ơn nhe.^_^

a)

\(\begin{array}{l}A(x) = {x^3} + \dfrac{3}{2}x - 7{x^4} + \dfrac{1}{2}x - 4{x^2} + 9\\ =  - 7{x^4} + {x^3} - 4{x^2} + \left( {\dfrac{3}{2}x + \dfrac{1}{2}x} \right) + 9\\ =  - 7{x^4} + {x^3} - 4{x^2} + 2x + 9\\B(x) = {x^5} - 3{x^2} + 8{x^4} - 5{x^2} - {x^5} + x - 7\\ = \left( {{x^5} - {x^5}} \right) + 8{x^4} + \left( { - 3{x^2} - 5{x^2}} \right) + x - 7\\ = 0 + 8{x^4} + ( - 8{x^2}) + x - 7\\ = 8{x^4} - 8{x^2} + x - 7\end{array}\)

b) * Đa thức A(x):

+ Bậc của đa thức là: 4

+ Hệ số cao nhất là: -7

+ Hệ số tự do là: 9

* Đa thức B(x):

+ Bậc của đa thức là: 4

+ Hệ số cao nhất là: 8

+ Hệ số tự do là: -7

a)

\(\begin{array}{l}P(x) = 5{x^3} + 2{x^4} - {x^2} + 3{x^2} - {x^3} - 2{x^4} - 4{x^3}\\ = \left( {2{x^4} - 2{x^4}} \right) + \left( {5{x^3} - {x^3} - 4{x^3}} \right) + \left( { - {x^2} + 3{x^2}} \right)\\ = 0 + 0 + 2{x^2}\\ = 2{x^2}\\Q(x) = 3x - 4{x^3} + 8{x^2} - 5x + 4{x^3} + 5\\ = \left( { - 4{x^3} + 4{x^3}} \right) + 8{x^2} + \left( {3x - 5x} \right) + 5\\ = 0 + 8{x^2} + ( - 2x) + 5\\ = 8{x^2} - 2x + 5\end{array}\)

b) P(1) = 2.1² = 2

P(0) = 2. 0² = 0

Q(-1) = 8.(-1)² – 2.(-1) +5 = 8 +2 +5 =15

Q(0) = 8.0² – 2.0 + 5 = 5

\(\begin{array}{l}A + B = (6{x^4} - 4{x^3} + x - \dfrac{1}{3}) + ( - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} - 4{x^3} + x - \dfrac{1}{3} - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3}\\ = (6{x^4} - 3{x^4}) + ( - 4{x^3} - 2{x^3}) - 5{x^2} + (x + x) + ( - \dfrac{1}{3} + \dfrac{2}{3})\\ = 3{x^4} - 6{x^3} - 5{x^2} + 2x + \dfrac{1}{3}\\A - B = (6{x^4} - 4{x^3} + x - \dfrac{1}{3}) - ( - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} - 4{x^3} + x - \dfrac{1}{3} + 3{x^4} + 2{x^3} + 5{x^2} - x - \dfrac{2}{3}\\ = (6{x^4} + 3{x^4}) + ( - 4{x^3} + 2{x^3}) + 5{x^2} + (x - x) + ( - \dfrac{1}{3} - \dfrac{2}{3})\\ = 9{x^4} - 2{x^3} + 5{x^2} - 1\end{array}\)\(\begin{array}{l}A + B = (6{x^4} - 4{x^3} + x - \dfrac{1}{3}) + ( - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} - 4{x^3} + x - \dfrac{1}{3} - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3}\\ = (6{x^4} - 3{x^4}) + ( - 4{x^3} - 2{x^3}) - 5{x^2} + (x + x) + ( - \dfrac{1}{3} + \dfrac{2}{3})\\ = 3{x^4} - 6{x^3} - 5{x^2} + 2x + \dfrac{1}{3}\\A - B = (6{x^4} - 4{x^3} + x - \dfrac{1}{3}) - ( - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} - 4{x^3} + x - \dfrac{1}{3} + 3{x^4} + 2{x^3} + 5{x^2} - x - \dfrac{2}{3}\\ = (6{x^4} + 3{x^4}) + ( - 4{x^3} + 2{x^3}) + 5{x^2} + (x - x) + ( - \dfrac{1}{3} - \dfrac{2}{3})\\ = 9{x^4} - 2{x^3} + 5{x^2} - 1\end{array}\)

a. \(x^4-5x^3+4x-5-x^4+3x^2+2x+1\)

\(=-5x^3+3x^2+6x-4\)

b. \(R\left(x\right)=x^4-5x^3+4x-5-\left(-x^4+3x^2+2x+1\right)\)

\(=x^4-5x^3+4x-5+x^4-3x^2-2x-1\)

\(=2x^4-5x^3-3x^2+2x-6\)

a) $P(x)+Q(x)$ 

$=\left(x^4-5x^3+4x-5\right)+\left(-x^4+3x^2+2x+1\right)$

$=x^4-5x^3+4x-5-x^4+3x^2+2x+1$

$=\left(x^4-x^4\right)-5x^3+3x^2+(4x+2x)+(1-5)$

$=-5x^3+3x^2+6x-4$

b) $R(x)=P(x)-Q(x)$

$=\left(x^4-5x^3+4x-5\right)-\left(-x^4+3x^2+2x+1\right)$

$=x^4-5x^3+4x-5+x^4-3x^2-2x-1$

$=\left(x^4+x^4\right)-5x^3-3x^2+(4x-2x)+(-1-5)$

$=2x^4-5x^3-3x^2+2x-6$

Tham khảo:

Cách 1 :

Ta có P(x) - Q(x)

= 2x³ – 9x² + 5 – (2x² + 4x³ – 7x)

= 2x³ – 9x² + 5 – 2x² – 4x³ + 7x

= (2x³ – 4x³) + (-9x² – 2x²) + 7x + 5

= -2x³ – 11x² + 7x + 5

Cách 2 :

P(x) = 2x³ – 9x² + 5

Q(x) = 4x³ + 2x² – 7x

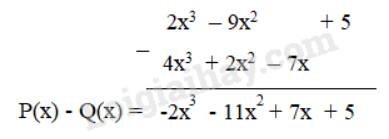
Để thu gọn và sắp xếp các hạng tử của mỗi đa thức, ta cần thực hiện các bước sau:
Đối với đa thức P(x): P(x) = (4x + 1 - x^2 + 2x^3) - (x^4 + 3x - x^3 - 2x^2 - 5) = 4x + 1 - x^2 + 2x^3 - x^4 - 3x + x^3 + 2x^2 + 5 = -x^4 + 3x^3 + x^2 + x + 6
Đối với đa thức Q(x): Q(x) = 3x^4 + 2x^5 - 3x - 5x^4 - x^5 + x + 2x^5 - 1 = 2x^5 - x^5 + 3x^4 - 5x^4 + x - 3x - 1 = x^5 - 2x^4 - 2x - 1
Sau khi thu gọn và sắp xếp các hạng tử, ta có: P(x) = -x^4 + 3x^3 + x^2 + x + 6 Q(x) = x^5 - 2x^4 - 2x - 1

a: \(P\left(x\right)=\left(4x+1-x^2+2x^3\right)-\left(x^4+3x-x^3-2x^2-5\right)\)

\(=4x+1-x^2+2x^3-x^4-3x+x^3+2x^2+5\)

\(=-x^4+3x^3+x^2+x+6\)

\(Q\left(x\right)=3x^4+2x^5-3x-5x^4-x^5+x+2x^5-1\)

\(=\left(2x^5-x^5+2x^5\right)+\left(3x^4-5x^4\right)+\left(-3x+x\right)-1\)

\(=-x^5-2x^4-2x-1\)

b: Bạn ghi lại đề đi bạn