Nếu tất cả các đường chéo của đa giác đều 12 cạnh được vẽ thì số đường chéo là:
A.121
B.66
C.132
D. 54
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu tất cả các đường chéo của 1 đa giác đều 12 cạnh được vẽ thì số đường chéo là : 54 đường chéo
Cứ 22 đỉnh của đa giác sẽ tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).
Khi đó có C212=66C122=66 đoạn thẳng.
Trong 6666 đoạn thẳng trên có 1212 đoạn thẳng là cạnh của đa giác nên:
Số đường chéo là: 66−12=5466−12=54.

Cứ hai đỉnh của đa giác ![]() đỉnh tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).
đỉnh tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).
Khi đó số đường chéo là: 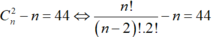
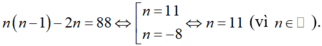
Chọn A.

Cứ hai đỉnh của đa giác n n ∈ ℕ , n ≥ 3 đỉnh tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).Do đó,đa giác có tất cả C n 2 đường chéo và cạnh
Đa giác n thì có n cạnh nên số đường chéo của đa giác là:
C n 2 − n = 44 ⇔ n ! n − 2 ! .2 ! − n = 44 ⇒ n ( n − 1 ) 2 − n = 44
⇔ n n − 1 − 2 n = 88 ⇔ n 2 − 3 n − 88 = 0 ⇔ n = 11 n = − 8 ⇔ n = 11 (vì n ∈ ℕ ).
Chọn đáp án A.

Ta có: ó n2 – 3n – 108 = 0
ó n2 – 12n + 9n – 108 = 0
ó n(n – 2) + 9 (n – 12) = 0
ó (n – 12) (n + 9) = 0
⇔ n − 12 = 0 n + 9 = 0
⇔ n = 12 ( t m ) n = − 9 ( k t m )
Số cạnh của đa giác là 12
Đáp án cần chọn là: D

a) Số đường chéo của đa giác đó :
\(\frac{\left(8-3\right).8}{2}=20\)( đường chéo )
b) Tổng số đo các góc của đa giác là :
\(108.\left(8-2\right)=108.6=1080\)độ
c) Số đo mỗi góc của đa giác đều 8 cạnh :
\(1080:8=135\)độ

Chọn B
Gọi A là biến cố lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C)
Số đường chéo của đa giác đều 20 đỉnh là
C
20
2
- 20 = 170. Khi đó, ta có số cách lấy ra 2 đường chéo trong số 170 đường là ![]()
Để có hai đường chéo cắt nhau tại một điểm nằm trong đường tròn (C) thì hai đường chéo đó phải là đường chéo của tứ giác có 4 đỉnh là đỉnh của đa giác đều 20 đỉnh. Do đó, số cách lấy ra 2 đường chéo có giao điểm nằm trong đường tròn tâm O là C 20 4 = 4845
Vậy xác suất lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C) là
![]()
a) Tính số đường chéo của đa giác có 24 cạnh
b) Tính số cạnh của đa giác biết đường chéo là 170 đường

a) \(\frac{\left(24-3\right).24}{2}=252\)đường chéo
b) \(\left(n-3\right).n=340\)
\(n^2-3n=340\)
\(n^2-3n-340=0\)
\(n^2-20n+17n-340=0\)
\(n\left(n-20\right)+17\left(n-20\right)\)
\(\left(n+17\right)\left(n-20\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}n+17=0\\n-20=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}n=-17\\n=20\end{cases}}\)
n = -17 ( loại )
n = 20 ( nhận )
Vậy n = 20 hay số cạnh của đa giác là 20
1 Đa giác có n cạnh có :
- Số đường chéo từ 1 đỉnh là : (n - 3)
- Số đỉnh là n
Do 1 đường chéo nối 2 đỉnh
=> 1 Đa giác có n cạnh có n(n - 3)/2 đường chéo
biết tổng số đường chéo là 170
=> n(n - 3)/2 = 170
=> n² - 3n - 340 = 0
∆ = (-3)² - 4.(-340) = 1369
=> √∆ = 37
=> n = ... (tự giải)
Cứ đỉnh của đa giác sẽ tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).
Khi đó có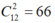 cạnh.
cạnh.
Số đường chéo là 66-12=54.
Chọn D.