Cho đoạn thẳng AB. Vẽ các cung tâm A và B có cùng bán kính sao cho chúng cắt nhau tại C và D. chứng minh rằng CD là đường trung trực của AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét hai tam giác ACD và BCD có:
AC = BC (gt)
AD = BD (gt)
CD: cạnh chung
Vậy: \(\Delta ACD=\Delta BCD\left(c-c-c\right)\)
Suy ra: \(\widehat{C_1}=\widehat{C_2}\) (hai góc tương ứng)
Xét hai tam giác ACH và BCH có:
AC = BC (gt)
\(\widehat{C_1}=\widehat{C_2}\) (cmt)
CH: cạnh chung
Vậy: \(\Delta ACH=\Delta BCH\left(c-g-c\right)\)
Suy ra: \(\widehat{H_1}=\widehat{H_2}\), HA = HB
Mà \(\widehat{H_1}+\widehat{H_2}=180^o\)
Nên \(\widehat{H_1}=\widehat{H_2}\) = 90o
Do đó: \(CH\perp AB\)
Vì \(CD\perp AB\)và HA = HB nên CD là đường trung trực của AB.

Hướng dẫn, tự vẽ hình:
Trung tâm A và B cùng bán kính
=> CA = CB DA = DB
Hai điểm C D cách đều 2 điểm A B nên CD là đường trung trực của AB.
Cung tâm A và cung tâm B có cùng bán kính
\(\Rightarrow\)CA = CB
Và DA = DB
Hai điểm C và D cách đều 2 điểm A và B nên CD là đường trung trực của AB ( đpcm )

Lời giải:
Bài 1:
Gọi H là giao điểm của AB và CD
Nối AC, AD,BC,BD
Xét ΔACD và ΔBCD, ta có:
AC = BC
(bán kính hai cung tròn bằng nhau)
AD = BD
CD cạnh chung
Suy ra: ΔACD= ΔBCD(c.c.c)
Suy ra: ∠C2 =∠C2 (hai góc tương ứng)
Xét hai tam giác AHC và BHC. Ta có:
AC = BC (bán kính hai cung tròn bằng nhau)
∠C2 =∠C2 (chứng minh trên)
CH cạnh chung
Suy ra: ΔAHC= ΔBHC(c.g.c)
Suy ra: AH = BH (hai cạnh tương ứng) (1)
Ta có : ∠H1 =∠H2 (hai góc tương ứng)
∠H1 + ∠H2 =180° (hai góc kề bù)
Suy ra: ∠H1 =∠H2 =90° => CD ⊥ AB (2)
Từ (1) và (2) suy ra CD là đường trung trực của AB
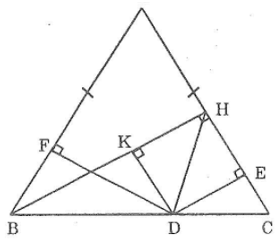
bài 2
Kẻ DK ⊥ BH
Ta có: BH ⊥AC(gt)
Suy ra: DK // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song)
=> ∠KDB =C (hai góc đồng vị)
VìΔABC cân tại A nên ∠B =∠C (tính chất tam giác cân)
Suy ra: ∠KDB =B
Xét hai tam giác vuông BFD và DKB, ta có:
∠BFD =∠DKB
BD cạnh huyền chung
∠FBD =∠KDB (chứng minh trên)
Suy ra:ΔBFD=ΔDKB(cạnh huyền góc nhọn)
=> DF = BK (hai cạnh tương ứng)(1)
Nối DH. XétΔDEHvàΔDKH, ta có:
∠DEH =∠DKH =90°
DH cạnh huyền chung
∠EHD =∠KDH (hai góc so le trong)
Suy ra:ΔDEH=ΔDKH( cạnh huyền , góc nhọn)
Suy ra: DE = HK ( hai cạnh tương ứng) (2)
Mặt khác : BH = BK + KH (3)
Từ (1), (2) và (3) suy ra: DF = DE = BH

Bạn chỉ cần viết lại khúc từ cung tròn tâm A đến ở C và D rồi suy ra AC=AB=AD=BD=BC là đc nhé còn lại tự giải

ta có : mình vẽ ko đúng lắm nhé
xét tam giác acm và tam giác bcm
có:am=bm(cùng bằng bán kính)
chung cm
bc=ca(m là trung điểm của ab)
vậy tam giac acm băng tam giác bcm (c.c.c)
vậy góc cma=góc cmb(2 góc tương ứng)
vì acb=180o mà cm nằm giữa ca và cb
vậy góc cma= góc cmb=góc acb/2=1800/2=90o
vậy góc cma và cmb vuông
vậy cm vuông góc với ab

Xét ΔABC và ΔABD, ta có:
AC = AD (bằng bán kính đường tròn (A))
Ab cạnh chung
BC = BD (bằng bán kính đường tròn (B))
Suy ra: ΔABC = ΔABD (c.c.c)

Xét ΔACD và ΔBCD, ta có:
AC = BC (= AB)
CD cạnh chung
AD = BD (= AB)
Suy ra: ΔACD = ΔBCD(c.c.c)


a) Xét tam giác NMA và NMB có:
\(MA=MB\left(gt\right)\)
\(NM\) là cạnh chung.
\(NA=NB\) (đường tròn tâm A và B cùng bán kính cắt nhau)
\(\Rightarrow\Delta NMA=\Delta NMB\left(c.c.c\right)\) (1)
b) Vì \(\widehat{NMA}=\widehat{NMB}\) (từ 1) và 2 góc trên là 2 góc kề bù nên \(\widehat{NMA}=\widehat{NMB}=90^o\)
Vậy \(NM\perp AB\)
c) \(NA=NB\) (từ 1)
\(BM=\dfrac{AB}{2}=\dfrac{12}{2}=6\left(cm\right)\)
Chu vi tam giác NMB:
\(10+8+6=24\left(cm\right)\)
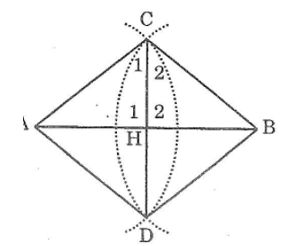
Gọi H là giao điểm của AB và CD
Nối AC, AD,BC,BD
Xét ΔACD và ΔBCD, ta có:
AC = BC
(bán kính hai cung tròn bằng nhau)
AD = BD
CD cạnh chung
Suy ra: ΔACD = ΔBCD(c.c.c)
Suy ra: ∠C1 = ∠C2 (hai góc tương ứng)
Xét hai tam giác AHC và BHC. Ta có:
AC = BC (bán kính hai cung tròn bằng nhau)
∠C1 = ∠C2 (chứng minh trên)
CH cạnh chung
Suy ra: ΔAHC = ΔBHC(c.g.c)
Suy ra: AH = BH (hai cạnh tương ứng) (1)
Ta có : ∠H1 = ∠H2 (hai góc tương ứng)
∠H1 + ∠H2 =180° (hai góc kề bù)
Suy ra: ∠H1 = ∠H2 = 90o ⇒ CD ⊥ AB (2)
Từ (1) và (2) suy ra CD là đường trung trực của AB