Cho phương trình ax + by = c với a ≠ 0; b ≠ 0. Chọn câu đúng nhất.
A. Phương trình đã cho luôn có vô số nghiệm
B. Tập nghiệm của phương trình được biểu diễn bởi đường thẳng d: ax + by = c
C. Tập nghiệm của phương trình là S = x ; − a b x + c b | x ∈ ℝ
D. Cả A, B, C đều đúng



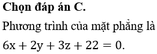
Phương trình bậc nhất hai ẩn ax + by = c luôn có vô số nghiệm
Tập nghiệm của phương trình được biểu diễn bởi đường thẳng d: ax + by = x
Ta có với a ≠ 0; b ≠ 0 thì ax + by = c ⇔ by = −ax + c ⇔ y = − a b x + c b
Nghiệm của phương trình là S = x ; − a b x + c b | x ∈ ℝ
Vậy cả A, B, C đều đúng
Đáp án: D