Cho hàm số: y = x 2 - 2 x x + 1 C
a) Đạo hàm của hàm số đã cho tại x=1 là:
A. 1/4
B. (-1)/2
C. 0
D. 1/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
5 tháng 8 2023
\(y'_1=-\dfrac{2}{\left(x-1\right)^2}\) nghịch biến trên R/{1}
\(y'_2=-3x^2+2x-3\) có nghiệm khi y' = 0
\(y'_3=4x^3+4x\) có nghiệm khi y' = 0
Vậy không có hàm số đơn điệu trên R.
18 tháng 12 2023
đơn điệu trên R là sao bạn? bạn chỉ mk cách nhận bt đc ko?
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2021
Để hàm số có đạo hàm tại 1 điểm thì nó phải liên tục tại điểm đó đồng thời đạo hàm trái bằng đạo hàm phải
\(\lim\limits_{x\rightarrow0^-}\left(2ax+1\right)=1\)
\(\lim\limits_{x\rightarrow0^+}\left(x^2+ax+1\right)=1\)
\(\Rightarrow\) Hàm liên tục tại \(x=1\)
\(y'\left(0^+\right)=2a\)
\(y'\left(0^-\right)=\left(2x+a\right)_{x=0^-}=a\)
Hàm có đạo hàm tại x=0 \(\Leftrightarrow2a=a\Leftrightarrow a=0\)
15 tháng 9 2023
1) \(f\left(x\right)=2x-5\)
\(f'\left(x\right)=2\)
\(\Rightarrow f'\left(4\right)=2\)
2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)
\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)
CM
15 tháng 7 2019
Chọn C.
Phương pháp : Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải :
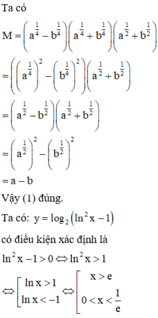
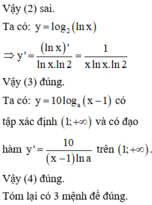
a) với ∆x là số gia của đối số tại x=1, ta có
Δ y = ( 1 + Δ x ) 2 − 2 ( 1 + Δ x ) 1 + Δ x + 1 − 1 − 2 1 + 1 = 1 + 2 Δ x + ( Δ x ) 2 − 2 − 2 Δ x 2 + Δ x + 1 2 = ( Δ x ) 2 − 1 2 + Δ x + 1 2 = 2 ( Δ x ) 2 − 2 + 2 + Δ x 2 ( 2 + Δ x ) = 2 ( Δ x ) 2 + Δ x 2 ( 2 + Δ x ) = ( 2 Δ x + 1 ) . Δ x 2 ( 2 + Δ x ) Δ y Δ x = 2 Δ x + 1 2 ( 2 + Δ x )
Vậy y’(1) =1/4.
Đáp án A