Cho hai điểm A, B cố định. Từ A vẽ các tiếp tuyến với các đường tròn tâm B có bán kính không lớn hơn AB. Tìm quỹ tích các tiếp điểm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


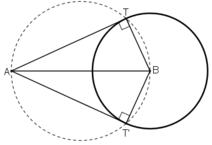
Dự đoán: Quỹ tích là đường tròn đường kính AB.
Chứng minh:
+ Phần thuận:
AT là tiếp tuyến của đường tròn tâm B
⇒ AT ⊥ BT
⇒ 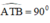
⇒ T thuộc đường tròn đường kính AB.
+ Phần đảo:
Lấy T thuộc đường tròn đường kính AB
⇒ 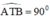
⇒ AT ⊥ TB và BT < AB
⇒ AT tiếp xúc với đường tròn tâm B, bán kính BT < BA.
Kết luận: Quỹ tích các tiếp điểm là đường tròn đường kính AB.
Kiến thức áp dụng
+ Thông thường, bài toán quỹ tích ta làm theo các bước:
1, Dự đoán quỹ tích
2, Chứng minh quỹ tích: gồm Phần thuận và Phần đảo
3, Kết luận.
+ Quỹ tích các điểm nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.

- Trường hợp các đường tròn tâm B có bán kính BA. Tiếp tuyến BA vuông góc với bán kính BT tại tiếp điểm T.
Do AB cố định nên quỹ tích của T là đường tròn đường kính AB.
- Trường hợp các đường tròn tâm B có bán kính lớn hơn BA: quỹ tích là tập hợp rỗng.
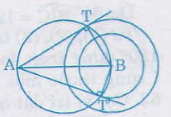

a: góc OBA+góc OCA=180 độ
=>OBAC nội tiếp
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>AH*AO=AB^2
Xét ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạng với ΔAEB
=>AB^2=AD*AE=AH*AO

Đề đúng không vậy bạn? Chỉ có thế thôi hả? \(AO⊥BC\) là hiển nhiên mà! Có gì phải CM?

a: Xét tứ giác AHMO có \(\widehat{HAO}+\widehat{HMO}=180^0\)
nên AHMO là tứ giác nội tiếp
Xét (O) có
HM là tiếp tuyến
HA là tiếp tuyến
Do đó: HM=HA và OH là tia phân giác của góc MOA(1)
Xét (O) có
KM là tiếp tuyến
KB là tiếp tuyến
Do đó: KM=KB và OK là tia phân giác của góc MOB(2)
Ta có: HM+MK=HK
nên HK=HA+KB
b: Từ (1) và (2) suy ra \(\widehat{HOK}=\dfrac{1}{2}\left(\widehat{MOA}+\widehat{MOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
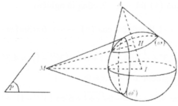

Dự đoán: Quỹ tích là đường tròn đường kính AB.
Chứng minh:
+ Phần thuận:
AT là tiếp tuyến của đường tròn tâm B
⇒ AT ⊥ BT
⇒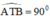
⇒ T thuộc đường tròn đường kính AB.
+ Phần đảo:
Lấy T thuộc đường tròn đường kính AB
⇒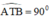
⇒ AT ⊥ TB và BT < AB
⇒ AT tiếp xúc với đường tròn tâm B, bán kính BT < BA.
Kết luận: Quỹ tích các tiếp điểm là đường tròn đường kính AB.