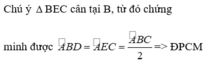Cho tam giác ABC. Tia phân giác góc B cắt AC ở D . Trên tia đối của tia BA lấy điểm E sao cho BE = BC. Chứng minh BD // EC (mình đang rất cần mong các bạn giải giúp. Xin cảm ơn)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 10 2019
Ta có: BD là tia phân giác của ∠ABC (giả thiết)
Suy ra: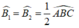 
(1)
Lại có: BE = BC (giả thiết)
=>∆BEC cân tại B (theo định nghĩa)
Suy ra: ∠E= ∠BCE (tính chất tam giác cân)
∆BEC có ABC là góc ngoài đỉnh B
=>∠ABC= ∠E + ∠BCE (tính chất góc ngoài tam giác)
Suy ra: ∠ABC=2∠E
Hay ∠E = (1/2)∠ABC (2)
Từ (1) và (2) suy ra: ∠E = ∠B1 = (1/2)∠ABC
Vậy BD // CE (vì có cặp góc ở vị trí đồng vị bằng nhau)
T
13 tháng 9 2019
Tự vẽ hình nha bn !
Ta có : ΔEBC cân B ( Vì BE=BC)
=> góc BEC = góc BCE ( Tam giác cân có hai góc ở đáy = nhau
mà góc BEC + góc BCE = góc ABC = 180 độ (t/c góc ngoài của Δ)
Ta lại có góc ABD = góc CBD (BD là tia p/g góc ABC)
=> 2 góc BEC = 2 góc CBD
=> góc BEC = góc CBD
mà 2 góc này ở vị trí đồng vị
=> BD//EC
13 tháng 9 2019
Tham khảo : Câu hỏi của Min Anna - Toán lớp 7 | Học trực tuyến