Chứng minh các đẳng thức sau với n ∈ N ∗ B n = 1 + 3 + 6 + 10 + . . . + n n + 1 2 = n n + 1 n + 2 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


tham khảo:
\(a) 2+5+8+...+(3n−1)=n(3n+1)2 (1) Đặt Sn=2+5+8+...+(3n−1) Với n=1 ta có: S1=2=1(3.1+1)2 Giả sử (1) đúng với n=k(k≥1), tức là Sk=2+5+8+...+(3k−1)=k(3k+1)2 Ta chứng minh (1) đúng với n=k+1 hay Sk+1=(k+1)(3k+4)2 Thật vậy ta có: Sk+1=2+5+8+...+(3k−1)+[3(k+1)−1]=Sk+3k+2=k(3k+1)2+3k+2=3k2+k+6k+42=3k2+7k+42=(k+1)(3k+4)2 Vậy (1) đúng với mọi k≥1 hay (1) đúng với mọi n∈N∗ b) 3+9+27+...+3n=12(3n+1−3) (2) Đặt Sn=3+9+27+...+3n=12(3n+1−3) Với n=1, ta có: S1=3=12(32−3) (hệ thức đúng) Giả sử (2) đúng với n=k(k≥1) tức là Sk=3+9+27+...+3k=12(3k+1−3) Ta chứng minh (2) đúng với n=k+1, tức là chứng minh Sk+1=12(3k+2−3) Thật vậy, ta có: Sk+1=3+9+27+...+3k+1=Sk+3k+1=12(3k+1−3)+3k+1=32.3k+1−32=12(3k+2−3)(đpcm) Vậy (2) đúng với mọi k≥1 hay đúng với mọi n∈N∗\)

Đặt vế trái bằng A n
Dễ thấy với n = 1 hệ thức đúng.
Giả sử đã có 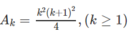
Ta có:
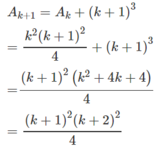

a, an+3-an+1=an.a(a2-1)=an(a-1)a(a+1)
Vì (a-1)a(a+1) là tích 3 số tự nhiên liên tiếp
=> (a-1)a(a+1) chia hết cho 2 và 3
Mà (2,3)=1
=>(a-1)a(a+1) chia hết cho 6
=> an(a-1)a(a+1) chia hết cho 6
=>đpcm
b, a3+5a=(a3-a)+6a=a(a2-1)+6a=(a-1)a(a+1)+6a
CM (a-1)a(a+1) chia hết cho 6
6a chia hết cho 6
=>(a-1)a(a+1)+6a chia hết cho 6
=>đpcm
c, a3+b3+c3-a-b-c=(a3-a)+(b3-b)+(c3-c)
đến đây dễ rồi, tự làm

iểm tra với n = 1
Giả sử đã có 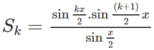
Viết S k + 1 = S k + sin ( k + 1 ) x sử dụng giả thiết quy nạp và biến đổi ta có
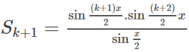
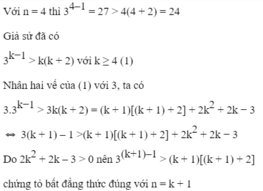
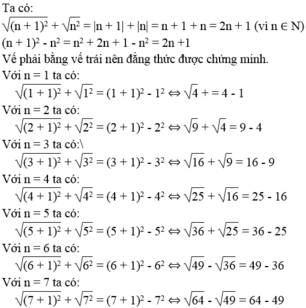
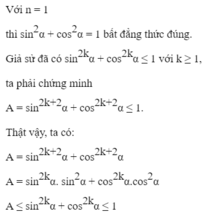
Kiểm tra với n = 1
Giả sử đã cho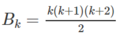
Ta cần chứng minh
bằng cách tính