Trong mặt phẳng Oxy cho hai điểm A ( 2 ; 3 ) , I ( 1 ; - 2 ) . Xác định tọa độ điểm B để I là trung điểm của AB.
A . ( 0 ; - 7 ) .
B . ( 3 2 ; 1 2 ) .
C. (1;2).
D . ( - 2 ; 1 ) .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có M ∈ O x nên M(m; 0) và A M → = m − 2 ; − 2 B M → = m − 5 ; 2 .
Vì A M B ^ = 90 0 suy ra A M → . B M → = 0 nên m − 2 m − 5 + − 2 .2 = 0.
⇔ m 2 − 7 m + 6 = 0 ⇔ m = 1 m = 6 ⇒ M 1 ; 0 M 6 ; 0 .
Chọn B.

Ta có M ∈ O x nên M( m; 0) và A M → = m − 2 ; − 2 B M → = m − 5 ; 2 .
Vì A M B ^ = 90 0 suy ra A M → . B M → = 0 nên m − 2 m − 5 + − 2 .2 = 0.
⇔ m 2 − 7 m + 6 = 0 ⇔ m = 1 m = 6 ⇒ M 1 ; 0 M 6 ; 0 .
Chọn B.

a) Khoảng cách từ gốc tọa độ \(O\left( {0;0} \right)\) đến điểm \(M\left( {3;4} \right)\) trong mặt phẳng tọa độ Oxy là:
\(OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{3^2} + {4^2}} = 5\)
b) Với hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy, ta có:\(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \)

Đáp án C
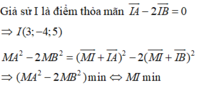
Suy ra M là hình chiếu vuông góc của I lên (Oxy) => I(3;-4;0)

Đáp án A.
Cách giải:
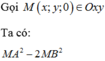
![]()
Thử lần lượt 4 đáp án thì ta thấy với M(3;-4;0)
thì M A 2 - 2 M B 2 = 3 là lớn nhất.
Chọn A.