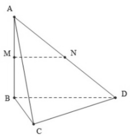
Cho tứ diện ABCD có các cạnh BA, BC, BD đôi một vuông góc với nhau: BA = 3a, BC =BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD Tính thể tích khối chóp C.BDNM.
A. V = 8 a 3
B. V = 2 a 3 3
C. V = 9 a 3 4
D. V = a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khối chóp C.BDNM có CB là đường cao nên có thể tích ![]() trong đó
trong đó
+ BC = 2a
+ Tứ giác BDNM là hình thang vuông tại B, M do MN là đường trung bình của tam giác ABD nên
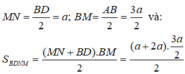
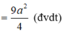
Thể tích của khối chóp C.BDNM là:
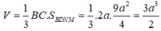

Đáp án C
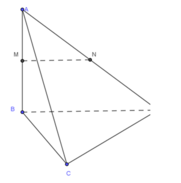
V C . B M N D V C . A B D = S B M N D S A B C = 3 4 ⇒ V C . B M N C = 3 4 V A B C D = 3 4 . 1 6 . B A . B C . B D = 3 2 a 3

Chọn A
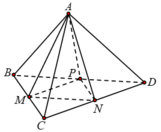
Cách 1: Khối tứ diện ABCD được chia thành bốn tứ diện có thể tích bằng nhau.
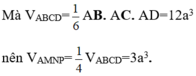
Cách 2:
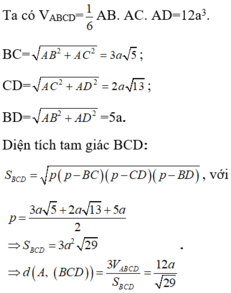
Mà M, N, P là trung điểm các cạnh BC, CD, BD nên hai tam giác BCD và MNP đồng dạng theo tỉ số
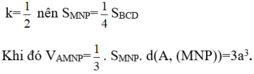

Đáp án C
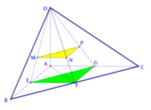
Gọi E,F,G lần lượt là trung điểm của các cạnh AB, BC, AC.
Khi đó:
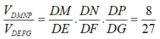
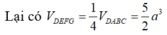
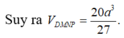
Đáp án C