Tìm số tự nhiên n thỏa mãn:
C n 0 1 . 2 + C n 1 2 . 3 + C n 2 3 . 4 + . . . + C n n n + 2 n + 1 = 2 100 - n - 3 n + 1 n + 2
A. 99
B. 100
C. 98
D. 101
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

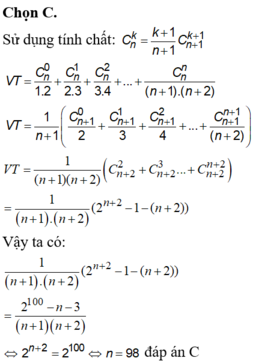

15.B
16.C
17.A
18.D
19.A
còn câu 20,21 mình sợ mình làm sai nên k ghi đáp án sorry bạn nha:(

Bài 2:
A = (a+b)(1/a+1/b)
Có: \(a+b\ge2\sqrt{ab}\)
\(\frac{1}{a}+\frac{1}{b}\ge2\sqrt{\frac{1}{ab}}\)
=> \(\left(a+b\right)\left(\frac{1}{a}+\frac{1}{b}\right)\ge2\sqrt{ab}.2\sqrt{\frac{1}{ab}}=4\)
=> ĐPCM
1.b)
Pt (1) : 4(n + 1) + 3n - 6 < 19
<=> 4n + 4 + 3n - 6 < 19
<=> 7n - 2 < 19
<=> 7n - 2 - 19 < 0
<=> 7n - 21 < 0
<=> n < 3
Pt (2) : (n - 3)^2 - (n + 4)(n - 4) ≤ 43
<=> n^2 - 6n + 9 - n^2 + 16 ≤ 43
<=> -6n + 25 ≤ 43
<=> -6n ≤ 18
<=> n ≥ -3
Vì n < 3 và n ≥ -3 => -3 ≤ n ≤ 3.
Vậy S = {x ∈ R ; -3 ≤ n ≤ 3}


a) \(4^n=2^{n+1}\)
\(\Rightarrow2^{2n}=2^{n+1}\)
\(\Rightarrow2n=n+1\)
\(\Rightarrow n=1\)
b) \(16=\left(n-1\right)^4\)
\(\Rightarrow2^4=\left(n-1\right)^4\)
\(\Rightarrow n-1=2\)
\(\Rightarrow n=3\)
c) \(125=\left(2n+1\right)^3\)
\(\Rightarrow5^3=\left(2n+1\right)^3\)
\(\Rightarrow2n+1=5\)
\(\Rightarrow2n=4\)
\(\Rightarrow n=2\)
a, 4n = 2n+1
(22)n = 2n+1
22n = 2n+1
2n = n + 1
2n - n = 1
n = 1
b, 16 = (n-1)4
24 = (n-1)4
2 = n-1
n = 3
c, 125 = (2n + 1)3
53 = (2n+1)3
5 = 2n + 1
2n = 4
n = 2

1 + 2 + 3 + 4 + ... + n = 171 ( n số hạng )
=> ( 1 + n ) . n : 2 = 171
=> \(n^2+n=342\)
=> \(n^2+n-342=0\)
=> \(\left(n-18\right)\left(n+19\right)=0\)
=> \(\orbr{\begin{cases}n-18=0\\n+19=0\end{cases}\Rightarrow\orbr{\begin{cases}n=18\\n=-19\end{cases}\Rightarrow}n=18}\)
Vậy n = 18

