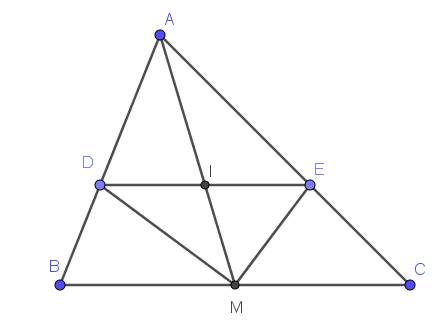
cho tam giác ABC nhọn có AB< AC và đường trung tuyến AM. Gọi D là trung điểm của AM, E là giao điểm BD và AC , F là trung điểm của EC. Biết AC = 9cm độ dài AE là ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 4 2017
a) VÌ DE//BC
SUY RA \(\frac{DN}{BM}=\frac{AN}{AM}\)VÀ \(\frac{NE}{MC}=\frac{AN}{AM}\)\(\Rightarrow\frac{DN}{BM}=\frac{NE}{MC}\)mà BM=MC(m là trung diểm) nên DN=NE
b) dễ thấy \(\frac{KN}{KC}=\frac{DN}{BC}\)VÀ\(\frac{SN}{SB}=\frac{NE}{BC}\)mà \(\frac{DN}{BC}=\frac{NE}{BC}\)(NE=DN)
\(\Rightarrow\frac{KN}{KC}=\frac{SN}{SB}\)áp dụng định lí talet ta suy ra KS//BC
AH
Akai Haruma
Giáo viên
13 tháng 1
Lời giải:
a. Áp dụng tính chất tia phân giác đối với tam giác $AMB, AMC$ thì:
$\frac{AD}{DB}=\frac{AM}{MB}$
$\frac{AE}{EC}=\frac{AM}{MC}$
Mà $MB=MC$ (do $M$ là trung điểm $BC$)
$\Rightarrow \frac{AD}{DB}=\frac{AE}{EC}$
$\Rightarrow DE\parallel BC$ (theo định lý Talet đảo)
b.
Tam giác $ABM$ có $DI\parallel BM$ (do $DE\parallel BC$) nên áp dụng định lý Talet:
$\frac{DI}{BM}=\frac{AI}{AM}$
Tam giác $ACM$ có $IE\parallel CM$ (do $DE\parallel BC$) nên áp dụng định lý Talet:
$\frac{IE}{MC}=\frac{AI}{AM}$
$\Rightarrow \frac{DI}{BM}=\frac{IE}{MC}$
Mà $BM=CM$ nên $DI=IE$
$\Rightarrow I$ là trung điểm $DE$>
17 tháng 5 2015
gọi giao điểm của AB vs DH là N; giao điểm của AC vs EH là M
xét tam giác DIN và tam giác HIN = nhau(c.g.c) suy ra IN hay IB là phân giác góc DIH
xét tam giác MKH và tam giác MKE = nhau (c.g.c) suy ra kc là phân giác góc MKE
ta lại có HA là phân giác góc HIK( NA,MA là phân giác góc ngoài)
mà góc AHC=90 độ(gt) suy ra HC là phân giác góc ngoài tam giác HIK tại đỉnh H
mà KC là phân giác góc ngoài tam giác HIK tại đỉnh K
suy ra IC là phân giác góc KIH
mà IB là phân giác góc DIH
góc KIH + góc DIH=180 độ( kề bù) suy ra góc BIC=90 độ
suy ra góc AIC=90 độ
góc AKB cm tương tự = 90 độ
12 tháng 2 2017
tuy mk ko biết chắc cách giải nhưng mk chắc bạn Đức làm sai rồi!