So sánh: sin 20o và sin 70o
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow\left[{}\begin{matrix}4x+10^0=x-20^0+k360^0\\4x+10^0=200^0-x+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=-30^0+k360^0\\5x=190^0+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-10^0+k120^0\\x=38^0+k72^0\end{matrix}\right.\) (\(k\in Z\))

Với 0 ° < α < 90 ° ta có α tăng thì sin α tăng
Ta có: 25 ° < 75 ° , suy ra sin 25 ° < sin 75 °

Tương tự câu 1
Chú ý các tỉ số lượng giác sin và cos có giá trị trong khoảng (0;1)

a: \(cos70=sin20\)
20<25
=>\(sin20< sin25\)
=>\(cos70< sin25\)
b: \(\dfrac{sin50}{cos40}=\dfrac{cos\left(90-50\right)}{cos40}=\dfrac{cos40}{cos40}=1\)
a) Ta có:
\(cos70^o=sin\left(90^o-70^o\right)=sin20^o\)
Ta so sánh \(sin25^o\) và \(sin20^o\)
\(25^o>20^o\Rightarrow sin25^o>sin20^o\)
\(\Rightarrow sin25^o>cos70^o\)
b) \(\dfrac{sin50^o}{cos40^o}\)
Ta có:
\(cos40^o=sin\left(90^o-40^o\right)=sin50^o\)
\(\Rightarrow\dfrac{sin50^o}{cos40^o}=\dfrac{sin50^o}{sin50^o}=1\)

a) Vì 20 ° < 70 ° n ê n sin 20 ° < sin 70 ° (góc tăng, sin tăng)
b) Vì 25 ° < 63 ° 15 ' n ê n cos 25 ° > cos 63 ° 15 ' (góc tăng, cos giảm)
c) Vì 73 ° 20 ' > 45 ° n ê n t g 73 ° 20 ' > t g 45 ° (góc tăng, tg tăng)
d) Vì 2 ° < 37 ° 40 ' n ê n c o t g 2 ° > c o t g 37 ° 40 ' (góc tăng, cotg giảm )


Theo a) sin 35 ° < tg 35 ° , mà khi góc lớn lên thì tang cũng lớn lên nên tg 35 ° < tg 38 ° . Vậy sin 35 ° < tg 38 ° .

cos\(60^0\)=sin(\(90^0-60^0\))=sin300cos600=sin(900−600)=sin300
Vì 300<450⇒sin300<sin450
⇒sin450>cos60
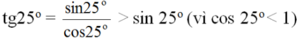
Vì 20o < 70o nên sin 20o < sin70o (góc tăng, sin tăng)