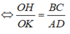Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, K, N, H lần lượt là chân đường vuông góc hạ từ O xuống các cạnh AB, BC, CD, DA. Chứng minh rằng: O H O K = B C A D
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì OM ⊥ AB và ON ⊥ CD, mà AB // CD nên suy ra M, O, N thẳng hàng.
Mặt khác, do AB // CD nên theo Định lí Ta-lét ta có:
Từ đó, theo tính chất của dãy tỉ số bằng nhau, ta có:

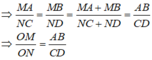

a;Vì AB//CD nên theo định lí Ta-lét ta có:
OA/OC=OB/ODOAOC=OBOD
⇒OA.OD=OC.OB⇒OA.OD=OC.OB
b;Xét ΔAOHΔAOH và ΔCOKΔCOKcó:
AHOˆ=CKO=90oˆAHO^=CKO=90o^
AOHˆ=COKˆAOH^=COK^ (hai góc đối đỉnh)
⇒ΔAOH ΔCOK(g.g)⇒ΔAOH ΔCOK(g.g)
⇒OAOC=OHOK(1)⇒OAOC=OHOK(1)
Vì AB//CD nên theo hệ quả của định lí Ta-lét ta có
ABCD=OAOC(2)ABCD=OAOC(2)
Từ 1 và 2 ta có:
OHOK=ABCD

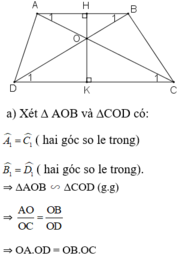
a) Xét hình thang ABCD có AB//CD => \(\widehat{A_1}=\widehat{C_1}\)và \(\widehat{B_1}=\widehat{D_1}\)
\(\Rightarrow\Delta AOB~\Delta COD\left(g.g\right)\)
=> \(\frac{OA}{OC}=\frac{OB}{OD}\Rightarrow OA\cdot OD=OB\cdot OC\)
b) Chứng minh \(\Delta AHO~\Delta CKO\left(g.g\right)\)
\(\frac{OH}{OK}=\frac{AH}{CK}\left(1\right)\)tương tự ta có:
\(\Delta BHO~\Delta DKO\left(g.g\right)\Rightarrow\frac{OH}{OK}=\frac{BH}{DK}\left(2\right)\)
Từ (1) (2) => \(\frac{OH}{OK}=\frac{AH}{CK}=\frac{BH}{DK}=\frac{AH+BH}{CK+DK}=\frac{AB}{CD}\)
vậy \(\frac{OH}{OK}=\frac{AB}{CD}\Rightarrow OH\cdot CD=OK\cdot AB\)

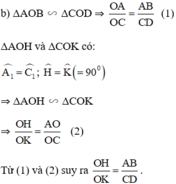
Từ O kẻ đường thẳng song song với AB và CD cắt AD tại E, cắt BC tại F.
Áp dụng kết quả chứng minh ở bài 14 ta có:
OE = OF
Từ đó, ta có:
S A E O = S B F O (1) (hai tam giác có cùng đường cao và hai đáy bằng nhau);
S D E O = S C F O (2)
Từ (1) và (2) suy ra : S O A D = S O B C (3)
Suy ra: OH.AD = OK.BC
⇔