Cho các số thực x , y thỏa mãn 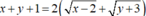. Giá trị lớn nhất của biểu thức bằng ...
Đọc tiếp
Cho các số thực x , y thỏa mãn 
. Giá trị lớn nhất của biểu thức 
bằng
K
Khách
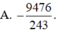
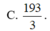
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PT
1
Những câu hỏi liên quan
Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu 
CM
1 tháng 3 2018
Đáp án C
Phương pháp:
Rút y theo x từ phương trình (1), thế vào phương trình (2) để tìm khoảng giá trị của x.
Đưa biểu thức P về 1 ẩn x và tìm GTLN, GTNN của biểu thức P.
Cách giải: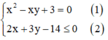 
Ta nhận thấy x = 0 không thỏa mãn phương trình (1), do đó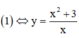 
thế vào (2):
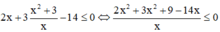
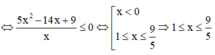
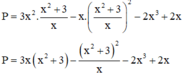
Sử dụng MTCT ta tính được
CM
5 tháng 11 2019
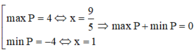
Giả thiết bài toán cho ta x > 0 và x 2 - 4 y 2 = 4
Không mất tính tổng quát, giả sử y ≥ 0 . Đặt t = x - y. Khi đó ta có 3 y 2 - 2 t y + 4 - t 2 = 0
Phương trình này có nghiệm khi và chỉ khi ∆ = 4 t 2 - 12 4 - t 2 ≥ 0 ⇒ t ≥ 3
Do x > 0 và y ≥ 0 nên t = x - y = x - y ≥ 3
Đáp án A
CM
11 tháng 11 2018
Ta có y= 3-x≥ 1 nên x≤ 2 do đó : x
Khi đó P= x3+ 2( 3-x) 2+ 3x2+4x( 3-x) -5x= x3+x2-5x+18
Xét hàm số f(x) = x3+x2-5x+18 trên đoạn [0 ; 2] ta có:
f ' ( x ) = 3 x 2 + 2 x - 5 ⇒ f ' ( x ) = 0 x ∈ ( 0 ; 2 ) ⇔
F(0) =18; f(1) = 15; f(2) =20
Vậy giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P lần lượt bằng 20 và 15.
Chọn B.
CM
1 tháng 12 2018
Đáp án C
Ta có x + y = 3 ⇒ y = 3 − x ≥ 1 ⇔ x ≤ 2 ⇒ x ∈ 0 ; 2
Khi đó P = f x = x 3 + 2 3 − x 2 + 3 x 2 + 4 x 3 − x − 5 x = x 3 + x 2 − 5 x + 18
Xét hàm số f x = x 3 + x 2 − 5 x + 18 trên đoạn 0 ; 2 , có f ' x = 3 x 2 + 2 x − 5
Phương trình 0 ≤ x ≤ 2 3 x 2 + 2 x − 5 = 0 ⇔ x = 1. Tính f 0 = 18 , f 1 = 15 , f 2 = 20
Vậy min 0 ; 2 f x = 15 , m a x 0 ; 2 f x = 20 hay P m a x = 20 và P min = 15
Đáp án đúng : D