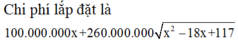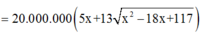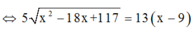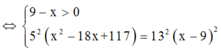Một nhóm cướp biển chôn báu vật của họ tại một kho ở trên một hòn đảo
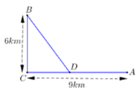
Trên đảo có một cây Cọ C và dọc bờ biển có hai tảng đá A và B. Từ cây Cọ C, một tên cướp biển bước đến tảng đá A, quay phải 90 độ rồi đi thẳng đến vị trí D sao cho AD = AC. Một tên cướp biển khác cũng từ cây Cọ C bước đến tảng đá B, quay trái 90 độ rồi đi thẳng đến vị trí E sao cho BE = BC. Nhóm cướp biển chôn báu vật tại trung điểm F của DE.Nhiều năm sau, một nhóm nhà thám hiểm có được tấm bản đồ kho báu và đã cùng nhau tìm đến hòn đảo nhưng chỉ thấy hai tảng đá nhưng không thấy vị trí cây cọ. Hỏi các nhà thám hiểm đã tìm kho báu bằng cách nào?Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

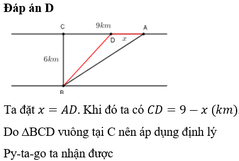
Đáp án B
Đặt A D = x → C D = 9 − x suy ra B D = 9 − x 2 + 36 km
Chi phí lắp đặt trên đoạn AD (trên bờ) là T 1 = 100 x triệu đồng
Chi phí lắp đặt trên đoạn DB (dưới nước) là T 2 = 260 9 − x 2 + 36 triệu đồng
Vậy tổng chi phí cần tính là T = T 1 + T 2 = 100 x + 260 9 − x 2 + 36 → f x
Xét hàm số f x = 100 x + 260 x 2 − 18 x + 117 trên đoạn 0 ; 9 → min 0 ; 9 f x = 2340
Dấu = xảy ra khi và chỉ khi x = 13 2 = 6 , 5 km

Đáp án là D.
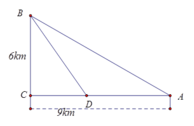
Đặt C D = x , x ∈ 0 ; 9 . Ta có B D = x 2 + 36
Chi phí xây dựng đường ống f x = 100 9 − x + 260 x 2 + 36
Ta có:
f ' x = − 100 + 260 x x 2 + 36 , c h o f ' x = 0 ⇔ 5 x 2 + 36 = 13 x ⇔ x = 5 2
f 0 = 2460 ; f 5 2 = 2340 ; f 9 ≈ 2812 , 33
Chi phí thấp nhất x = 5 2 . Khoảng cách từ A đến D là: 6,5km

Ta gọi 5 tên cướp biển là A, B, C, D, E (từ giá nhất đến trẻ nhất). Ta giải ngược từ dưới lên như sau.
Nếu chỉ có 2 tên cướp biển: D chia số tiền theo tỷ lệ 100:0 (lấy hết số tiền vàng về mình). Anh ta sẽ biểu quyết đồng ý và điều này đủ để phương án được thông qua.
Nếu chỉ có 3 tên cướp biển: C sẽ chia số tiền theo tỷ lệ 99 : 0 : 1. E sẽ chấp nhận phương án này (chỉ được có 1 đồng vàng), vì anh ta biết rằng trong trường hợp anh ta phản đối phương án, chỉ còn lại D và E thì anh ta sẽ chẳng được gì.
Nếu có 4 cướp biển: B chia tiền thành 99: 0 : 1: 0. Cũng lý luận như trên, ta thấy D sẽ ủng hộ phương án này. B cũng không nên dùng 1 đồng để mua chuộc C vì C biết rằng nếu anh ta không ủ hộ B, anh ta sẽ bỏ túi 99 đồng xu nếu B bị vứt xuống biển. B cũng không nên mua chuộc E vì E biết rằng nếu B bị vứt xuống biển và C chia tiền thì anh ta cũng sẽ được C chia cho 1 đồng.
Nếu có 5 cướp biển: A chia các đồng tiền theo tỷ lệ 98 : 0 : 1 : 0 : 1. Bằng cách cho C và E mỗi người một đồng tiền vàng (những người sẽ chẳng được gì nếu không đồng ý phương án của A), anh ta đảm bảo phương án sẽ được thông qua.
Ghi chú: Trong trường hợp cuối (cũng chính là trường hợp của đề bài) A không cho B tiền vì B biết rằng nếu anh ta không đồng ý phương án của A và A bị vứt xuống biển thì anh ta sẽ bỏ túi 99 đồng. Tương tự như vậy, anh ta sẽ không cho D một đồng tiền vàng, vì D biết nếu A thất bại thì B cũng cho D một đồng tiền vàng như A. Mà như thế thì do tính khát máu, D sẽ không bỏ phiếu cho A.

Đáp án B
Trước tiên ta xác định hàm số f(x) là hàm số tính thời gian người canh hải đăng phải đi.
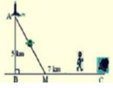
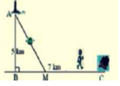
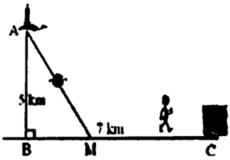
Đặt BM= x , CM =7-x-> A M = x 2 + 25 . Theo đề ta có ngưới canh hải đăng chèo từ A đến M trên bờ biển với v = 4km/h rồi đi bộ đến C với v = 6 km/h
⇒ f ( x ) = x 2 + 25 4 + 7 − x 6 = 3 x 2 + 25 − 2 x + 14 12 với x ∈ ( 0 ; 7 )
f ' ( x ) = 1 12 3 x x 2 + 25 − 2 f ' ( x ) = 0 ⇔ 3 x x 2 + 25 − 2 = 0 ⇔ 3 x − 2 x 2 + 25 = 0 ⇔ 2 x 2 + 25 = 3 x ⇔ 5 x 2 = 100 x ≥ 0 ⇔ x = ± 2 5 x ≥ 0 ⇔ x = 2 5
Vậy đoạn đường ngắn nhất thì giá trị phải nhỏ nhất
f ( 0 ) = 29 12 f ( 2 5 ) = 14 + 5 5 12 f ( 7 ) = 74 4
Vậy giá trị nhỏ nhất của f(x) là 14 + 5 5 12 tại x= 2 5
Nên thời gian đi ít nhât là BM= x = 2 5

Đáp án B
Trước tiên ta xác định hàm số f(x) là hàm số tính thời gian người canh hải đăng phải đi.
Đặt BM= x , CM =7-x ⇒ A M = x 2 + 25 . Theo đề ta có ngưới canh hải đăng chèo từ A đến M trên bờ biển với v = 4km/h rồi đi bộ đến C với v = 6 km/h
⇒ f ( x ) = x 2 + 25 4 + 7 − x 6 = 3 x 2 + 25 − 2 x + 14 12 với x ∈ ( 0 ; 7 )
f ' ( x ) = 1 12 3 x x 2 + 25 − 2 f ' ( x ) = 0 ⇔ 3 x x 2 + 25 − 2 = 0 ⇔ 3 x − 2 x 2 + 25 = 0 ⇔ 2 x 2 + 25 = 3 x ⇔ 5 x 2 = 100 x ≥ 0 ⇔ x = ± 2 5 x ≥ 0 ⇔ x = 2 5
Vậy đoạn đường ngắn nhất thì giá trị phải nhỏ nhất
f ( 0 ) = 29 12 f ( 2 5 ) = 14 + 5 5 12 f ( 7 ) = 74 4
Vậy giá trị nhỏ nhất của f(x) là 14 + 5 5 12 tại x= 2 5
Nên thời gian đi ít nhât là BM= x = 2 5

Đáp án A
Phương pháp: Sử dụng phương pháp hàm số.
Cách giải: Gọi độ dài đoạn MB là x ![]()
Tam giác ABM vuông tại B => ![]()
Thời gian người đó đi từ A tới C: 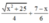
Xét hàm số f(x) 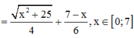

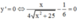
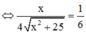
![]()
![]()
=> x = 2 5
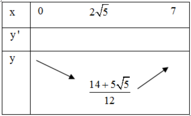
Vậy, để người đó đến C nhanh nhất thì khoảng cách từ B đến M là 2 5

Gọi BM=x km (0<x<7)
=> MC=7-x (km)
Ta có: \(AM = \sqrt {A{B^2} + B{M^2}} \)\( = \sqrt {16 + {x^2}} \left( {km} \right)\)
Thời gian từ A đến M là: \(\frac{{\sqrt {16 + {x^2}} }}{3}\left( h \right)\)
Thời gian từ M đến C là: \(\frac{{7 - x}}{5}\left( h \right)\)
Tổng thời gian từ A đến C là 148 phút nên ta có:
\(\begin{array}{l}\frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{148}}{{60}}\\ \Leftrightarrow \frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{37}}{{15}}\\ \Leftrightarrow \frac{{5\sqrt {16 + {x^2}} }}{{15}} + \frac{{3.\left( {7 - x} \right)}}{{15}} = \frac{{37}}{{15}}\\ \Leftrightarrow 5\sqrt {16 + {x^2}} + 3.\left( {7 - x} \right) = 37\\ \Leftrightarrow 5\sqrt {16 + {x^2}} = 16 + 3x\\ \Leftrightarrow 25.\left( {16 + {x^2}} \right) = 9{x^2} + 96x + 256\\ \Leftrightarrow 16{x^2} - 96x + 144 = 0\\ \Leftrightarrow x = 3\left( {tm} \right)\end{array}\)
Vậy khoảng cách từ vị trí B đến M là 3 km.